9 Beyond Behavioral Objectives: Problem Solving and Constructivism
“There are many ways to learn and many ways of encouraging different forms of learning with different ends in view. At the heart of the decision process, there must be a value judgment about how the mind should be cultivated to what end.” –Jerome Bruner

Introduction
Most experts agree that behavioral objectives have a place in the curriculum, but most experts agree that it is important to include other kinds of objectives that encourage critical and creative thinking (White, 2018). When engaging in problem-solving, constructivist, and experiential learning, it is important to go beyond behavioral objectives.
According to the Center for Teaching Excellence at the University of Waterloo, “True problem-solving is the process of applying a method – not known in advance – to a problem that is subject to a specific set of conditions and that the problem-solver has not seen before, to obtain a satisfactory solution.”
Wilson (2020) states that:
There are two alternate forms of writing objectives beyond behavioral ones – they are problems-solving objectives and expressive activities that lead to expressive outcomes [such as in the fine or visual arts, drama, etc.]. Teachers should know how to use these because they extend the artistry of the profession. More importantly, they can be crafted to provide students with powerful types of learning activities that encourage higher-level thinking skills and that are closely aligned to learning experiences in the real world.
In simpler terms, behavioral objectives refer to objectives that are measurable and observable as determined and stated prior to the lesson, and problem-solving objectives refer to objectives that are revealed as a result of student inquiry and self-directed learning. For more details about problem-solving and expressive objectives, access Wilson’s slide show at Beyond Behavioral Objectives.
Essential Questions
- Behavioral objectives have a place in curriculum, but it is also important to have non-behavioral objectives. Why?
- What are two alternative ways of writing objectives?
- What skills do students need to have to do problem-solving?
- What challenge is posed when working with both expert and novice problem-solvers?
Insight 9.1
Problem-solving can be an exciting and engaging way to teach because the students become more invested in learning that is creative, “hands-on” with a teacher as a “guide-on-the-side” and not just the “sage-on-the-stage.” As a classroom teacher, I discovered that students who were bored with the traditional read-and-answer-the-questions format became motivated and excited about learning when they were able to identify a problem, apply strategies to solve the problem, and work together for a solution. Students do not necessarily have the strategies initially, so sometimes there is a trial-and-error period that involves important learning about what does not work and why. One of the benefits of problem-solving is that the skills and strategies can be transferred to other subjects and even to the real world.
In one instance during a math lesson, the students were having difficulty with division, and they did not understand what 20 divided by five meant. In a small group, we counted out 20 beans, and I asked the students to pretend that there were five mice who each wanted beans, but they had to be divided evenly. The students decided that they could use five small paper plates, one for each mouse. The students divided the 20 beans, one at a time, and placed them onto the five plates. Voila! Each plate had four beans! It was a fair way to divide the 20 beans. I then showed the students how to write the equation: 20/5. Later, we looked at the inverse process: 4 x 5 = 20. That made sense to them, too. They then came up with their own problems and worked them out with beans and plates and their newly acquired problem-solving skills.
It would be very simple to write a behavioral objective for the first part of the lesson:
“The students will use 20 beans and five paper plates to solve the equation 20/ 5= 4,” but there would not be a way to write discrete behavioral objectives for the problems the students posed later. Creative thinking and problem-solving go beyond discrete objectives because the students are provided with a “window of opportunity” to pose and solve their own problems.
However, the complicating factor is that the objective was written prior to the lesson. Because there are multiple ways of solving the problem, several students might be able to get the correct answer using different methods: paper and pencil computation, separating the beans, etc. This would make an excellent discussion after the students shared their answers so they could see that problems can be solved in different ways. This concept fits the larger goal of problem-solving.
Problem-solving Through Constructivist Learning
In many traditional classrooms, teachers present the behavioral objectives and information to the students at the beginning of the lesson. This process is often effective and can be very appropriate because the teacher can present much information in a short period of time. It can be an efficient way of teaching although the students must absorb the information “upfront.” In constructivist teaching, the process becomes more meaningful because the students are more fully engaged in solving the problem, so there is a higher probability that they will retain the concepts.
When teaching focuses on students and challenging their perceptions, students report a deeper involvement with learning the subject (Trigwell, Prosser & Waterhouse, 2004). Proponents of constructivism believe that if teachers shift their teaching practices, especially in math and science, it will increase student achievement (Nyagah, 2017). The following insight illustrates how problem-solving and inquiry can be powerful learning models.
Insight 9.2
On September 11, 2001, Vicky, one of my teaching colleagues, had planned to teach a literacy lesson on Colorado history using multiple texts. When the news from New York was broadcast, everything in the 4th-grade classroom stopped.
“Why were the buildings in New York brought down?” one student asked.
“What happened to the people?” asked another.
The teacher answered the questions as best she could then promised the children they would learn more the next day. Vicky spent time that evening developing a unit on the events of September 11, and she chose books that would help 4th-grade students understand what had happened in the context of other accidental and purposeful events with tragic results, as well as books on New York as a center of trade, and the bravery of first responders and citizens in other situations. One group that she deemed most mature read screened articles about the causes of the September 11th tragedy.
The children were motivated to read about their topics. They asked and answered questions and discussed the new concepts they had learned. At the end of the unit, they shared what they learned from different sources and came up with five conclusions, beginning with “Sometimes things happen that we don’t understand, and we want to learn more about them.”
Vicky’s unit required the students to find out why the September 11th event, as well as events such as fires and collapsing bridges, had occurred, and what they learned as a result of reading about these topics. She said that at the end of the unit, the students had gained knowledge about what happened on September 11, as well as tragedies that had happened in other places, how brave people responded, and what they learned from the events. The problem-solving objectives were not stated at the beginning of the unit because it was uncertain at that time what the students would learn. Their discussions and critical thinking defined what was learned. I should note here that Vicky was a veteran teacher who was in communication with parents and had experience in guiding children in constructivist lessons.
For this experience, Vicky was guided by the following principles suggested by Honebein (1996), which summarize the seven pedagogical goals of constructivist learning environments:
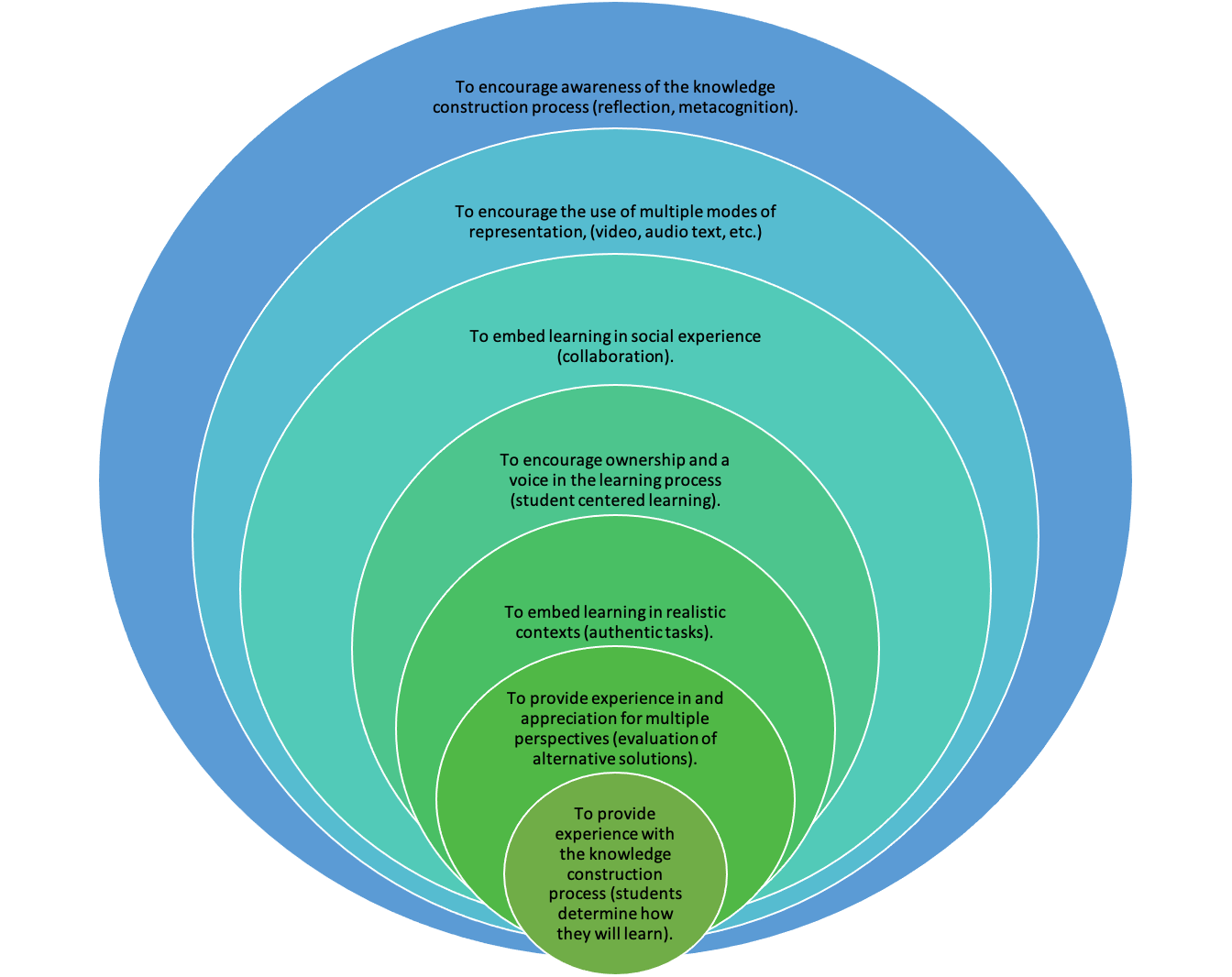
Teaching Problem Solving
The Vanderbilt Center For Teaching offers these additional “Tips and Techniques” for teaching problem-solving.

Content from the Vanderbilt Center for Teaching site is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.
Communicate
The Vanderbilt Center For Teaching offers these additional “Tips and Techniques” for teaching problem-solving.
- Have students identify specific problems, difficulties, or confusion. Don’t waste time working through problems that students already understand.
- If students are unable to articulate their concerns, determine where they are having trouble by asking them to identify the specific concepts or principles associated with the problem.
- Make students articulate their problem-solving process.
- In a one-on-one tutoring session, ask the student to work their problem out loud. This slows down the thinking process, making it more accurate and allowing them to access understanding of the process.
- When working with larger groups, ask students to provide a written, “two-column solution.”
- Have students write up their solution to a problem by putting all their calculations in one column and all of their reasoning (in complete sentences) in the other column.
- This helps them to think critically about their own problem solving and helps you to more easily identify where they may be having problems.
- Two-Column Solution (Math)
- Two-Column Solution (Physics)
Encourage Independence
- Model the problem-solving process rather than just giving students the answer. As you work through the problem, consider how a novice might struggle with the concepts, and make your thinking clear.
- Have students work through problems on their own. Ask directing questions or give helpful suggestions but provide only minimal assistance and only when needed to overcome obstacles.
- Don’t fear group work!
- Students can frequently help each other and talking about a problem helps them think more critically about the steps needed to solve the problem.
- Additionally, group work helps students realize that problems often have multiple solution strategies, some that might be more effective than others.
Be Sensitive
- Frequently, when working problems, students are unsure of themselves. This lack of confidence may hamper their learning.
- It is important to recognize this when students come to us for help and to give each student some feeling of mastery.
- Do this by providing positive reinforcement to let students know when they have mastered a new concept or skill.
Encourage Thoroughness and Patience
- Try to communicate that the process is more important than the answer so that the student learns that it is OK not to have an instant solution.
- This is learned through your acceptance of his/her pace of doing things, through your refusal to let anxiety pressure you into giving the right answer, and through your example of problem-solving through a step-by-step process.
Interactive Learning Activity (ILA) 9.0
Which problem-solving technique resonated with you? Was it something that “worked” for you or your students? Use the ILA Responses Group for your responses.
Expert vs. Novice Problem-Solvers
Experts (teachers) in a particular field are often so fluent in solving problems from that field that they can find it difficult to articulate the problem-solving principles and strategies they use to novices (students) in their field because these principles and strategies are second nature to the expert. To teach students problem-solving skills, a teacher should be aware of the principles and strategies of good problem-solving in his or her discipline.
The mathematician George Polya captured the problem-solving principles and strategies he used in his discipline in the book How to Solve It: A New Aspect of Mathematical Method (Princeton University Press, 1957). The book includes a summary of Polya’s problem-solving heuristic as well as advice on the teaching of problem-solving.

Novices in a particular field typically have not yet developed effective problem-solving principles and strategies. Helping students identify their own problem-solving errors is part of helping them develop effective problem-solving skills. Beverly Black and Elizabeth Axelson’s list of common problem-solving errors, adapted from Arthur Whimbey and Jack Lochhead’s book Problem Solving and Comprehension (Lawrence Erlbaum, 1999), provides useful insight into the mindset of a novice problem solver.
The Vanderbilt Center for Teaching has an Open Educational Resource at their Center for Teaching Guide that offers Tips and Techniques for Teaching Problem Solving.
An excellent video by Michael Arnold describes some very innovative ways to teach children how to solve problems, and how we can find the “Lost Einsteins.”
Insight 9.3
Lessons with objectives provide a solid structure for curriculum planning and lessons, but inquiry and problem-solving provide a different dimension for student learning that can motivate and engage student learning at a deep level.
Summary
Problem-solving and creative thinking can be an exciting way to teach and an engaging way for students to learn because it is connected to the real world.
While traditional learning holds to single answers, problem-solving can lead to multiple solutions and even new problems. Since the process is more important than the product, teachers function best if they have collaborative learning and a supportive classroom atmosphere that encourages risk-taking.
