"

38 Homework: Second Derivatives and Interpreting the Derivative

  1. Given each [latex]f(t)[/latex], describe in one sentence the meaning of [latex]f'(t)[/latex].
    1. Let [latex]f(t)[/latex] be the distance (in miles) an astronaut is from the surface of the earth as he blasts off towards space. Here [latex]t[/latex] is measured in hours.
      [latex]f'(t)[/latex] is the speed of the astronaut in miles per hour

      ans
    2. Let [latex]f(t)[/latex] be the number of gallons of diesel gasoline in the tank of a truck, with [latex]t[/latex] measured in hours.
      [latex]f'(t)[/latex] is how fast fuel is being burned, in gallons per minute. It could also represent how fast the fuel is being filled up at a gas station.

      ans
    3. Let [latex]f(t)[/latex] be the concentration of NaCl in parts per million within the cytoplasm of a cell. Here, [latex]t[/latex] is measured in minutes.
      [latex]f'(t)[/latex] is the rate the concentration of NaCl is increasing in parts per million per minute.

      ans
    4. Let [latex]f(t)[/latex] be the speed of a runner (in feet per second), and let [latex]t[/latex] be measured in seconds.
      [latex]f'(t)[/latex] is the acceleration of the runner, or the rate at which the runner’s speed is increasing in (feet per second) per second.

      ans
    5. Let [latex]f(t)[/latex] be the rate (in dollars per hour) that you are paid, where [latex]t[/latex] is measured in months.
      [latex]f'(t)[/latex] is like how fast are you getting raises, measured in (dollars per hour) per month.

      ans
  2. For each of the functions below, compute the derivative twice. That is, compute [latex]f'(t)[/latex], then take the derivative of [latex]f'(t)[/latex] to find [latex]f''(t)[/latex].
    1. [latex]f(t) = 5t^2 - 6t + 2[/latex]
      [latex]10t - 6[/latex], [latex]10[/latex]

      ans
    2. [latex]f(t) = t^3 + e^t - \sqrt{t}[/latex].
      [latex]3t^2 + e^t - 1/2 t^{-1/2}[/latex], [latex]6t + e^t + 1/4 t^{-3/2}[/latex]

      ans
    3. [latex]f(t) = \frac{1}{t}[/latex]
      [latex]-t^{-2}, 2 t^{-3}[/latex]

      ans
    4. [latex]f(t) = \sin(t)[/latex]
      [latex]\cos(t)[/latex], [latex](-\sin(t))[/latex]

      ans
    5. [latex]f(t) = (\sqrt{t} + 1)^2[/latex]
      [latex]1 + t^{-1/2}[/latex], [latex]-\frac{1}{2} t^{-3/2}[/latex]

      ans
  3. For each graph, circle any inflection points (if any). Label each region between the inflection points has having either a positive or negative second derivative.

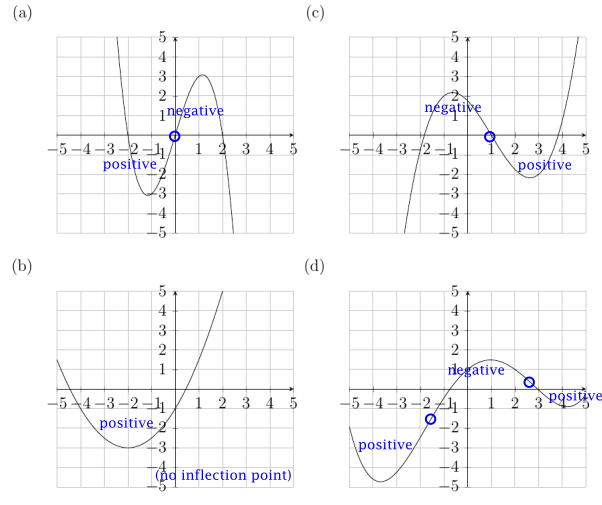
    ans
  4. A river bank is eroding. Let [latex]f(t)[/latex] be the metric tonnes of soil and rock material on day [latex]t[/latex]. Suppose [latex]f(t) = 0.05t^2 - 3t + 125[/latex] (this model is valid from [latex]t = 0[/latex] to [latex]t =30[/latex]) .

    1. What is [latex]f'(t)[/latex] measuring? What are the correct units?
      How quickly soil and rock are being lost due to erosion in metric tonnes per day.

      ans
    2. Sketch the derivative.
    3. Find the derivative
      [latex]0.1x - 3[/latex]

      ans
    4. How quickly is material being lost on day [latex]t = 5[/latex]? How quickly is material being lost on day [latex]t = 25[/latex]?
      [latex]2.5[/latex] metric tons per day on day [latex]5[/latex], [latex]0.5[/latex] metric tons per day on day [latex]25[/latex].

      ans
  5. The stock price for Math Nerds, Inc, over the course of an 8 hour trading day ([latex]t = 0[/latex] to [latex]t = 8[/latex]) is modeled by [latex]p(t) = -0.3t^3 + 3t^2 - 4t + 17[/latex] ([latex]p(t)[/latex] is measured in dollars).

    1. What is [latex]p'(t)[/latex] measuring? What is [latex]p''(t)[/latex] measuring? State the correct units for each.
      [latex]p'(t)[/latex] is the rate of change of the stock price in dollars per hour. [latex]p''(t)[/latex] is how quickly the stock price rate is speeding up or slowing down, measured in dollars per hour[latex]^2[/latex]

      ans
    2. Sketch the graph of [latex]p'(t)[/latex] and [latex]p''(t))[/latex].
    3. Compute [latex]p'(t)[/latex] and [latex]p''(t)[/latex].
      [latex]p'(t) = -0.9t^2 + 6t - 4[/latex], [latex]p''(t) = -1.8t + 6[/latex].

      ans
    4. How quickly is the stock gaining in price at [latex]t = 4[/latex]? How quickly is it losing value at [latex]t = 7[/latex]?
      Gaining at 5.6 dollars per hour at [latex]t = 4[/latex], but losing at a rate of [latex]-6.1[/latex] dollars per hour at [latex]t = 7[/latex]

      ans
    5. At [latex]t = 4[/latex], the stock price is clearly growing. But is growth speeding up or slowing down? How can you use the formula for [latex]p(t)[/latex], [latex]p'(t)[/latex], or [latex]p''(t)[/latex] to find out?
      We can plug [latex]t = 4[/latex] into [latex]p''(t)[/latex], to get an answer of [latex]-1.2[/latex] dollars per hour per hour, which means growth is slowing down.

      ans
  6. A tank has [latex]f(t)[/latex] liters of water at time [latex]t[/latex] measured in minutes, where [latex]f(t) = -2.2t^3 +27t^2- 120t + 500[/latex] (this model is valid [latex]t = 0[/latex] to [latex]t = 9[/latex]).

    1. Sketch the graphs of [latex]f'(t)[/latex] and [latex]f''(t)[/latex].
    2. What is [latex]f'(t)[/latex] measuring? What is the meaning of [latex]f''(t)[/latex]? Give the correct units.
      Imagine water is leaking out of a hole. [latex]f'(t)[/latex] is indirectly measuring the size of that hole, since it is measuring how quickly water is being lost in liters per minute. [latex]f''(t)[/latex] would relate to how quickly the hole is opening or closing, thus measuring how fast the rate is changing in liters per minute per minute.

      ans

License

Icon for the Creative Commons Attribution 4.0 International License

Informal Calculus Copyright © by Tyler Seacrest is licensed under a Creative Commons Attribution 4.0 International License, except where otherwise noted.

Share This Book