In derivative story problems, often you’re given a function that describes the amount of something, and you’re asked to find the rate of change. With integral story problems, the reverse is often true. You’ll be given a function the describes the rate of change over time, and you’ll be asked to get the amount.

Discussion: We know that distance is equal to velocity multiplied by time. So if we can figure out the train’s velocity, we can just multiply by [latex]800[/latex] seconds and get an answer. So here are some potential answers:

[latex]\begin{array}{cc} \text{Speed of the train (m/s)} &\text{Distance traveled (m)} \\ 0 & 0 \\ 10 & 8000 \\ 20 & 16000 \\ 30 & 24000 \\ 40 & 32000 \end{array}[/latex]

Why can’t we just go with [latex]40[/latex] meters per second? Because the train “eventually” gets up to [latex]40[/latex] meters per second doesn’t mean it was going [latex]40[/latex] meters per second the whole time — most of the trip it may have been going slower. So the answer of [latex]32,000[/latex] meters (or [latex]32[/latex] kilometers) is an upper bound, but isn’t the final answer. We need more information.

What this additional information is telling us is that there isn’t just a single velocity we can use and multiply by the [latex]800[/latex] seconds — instead, the velocity is changing all the time so there are lots of velocities. Since the train goes from [latex]0[/latex] to [latex]40[/latex] meters per second, can we just use the “average” which is [latex]20[/latex] meters per second? Well, let’s look at the speeds over time:

[latex]\begin{array}{cc} \text{Time (s)} &\text{Velocity given by $f(t) = \sqrt{2t}$ in m/s} \\ 0 & 0 \\ 100 & 14.1 \\ 200 & 20 \\ 300 & 24.5 \\ 400 & 28.3 \\ 500 & 31.6 \\ 600 & 34.6 \\ 700 & 37.4 \\ 800 & 40 \end{array}[/latex]

You can see the train spends much more time above 20 m/s than it does below, so that the train probably goes farther than [latex]800 \cdot 20 = 16000[/latex] meters ([latex]16[/latex] km).

What about the speed at time [latex]t = 400[/latex] which is [latex]28.3[/latex] m/s? Can we use this value? Well, let’s see what that would mean visually. That’s basically treating the speed at the half-way point like it is a constant velocity:

So if we use a velocity of [latex]28.3[/latex] meters per second, that would give a final distance of [latex]800 \cdot 28.3 \approx 22600[/latex] meters (22.6 km). But even this isn’t quite right. The train spends an equal amount of time slower than [latex]28.3[/latex] and faster than [latex]28.3[/latex], but the slow region (from time [latex]0[/latex] to time [latex]400[/latex]) is slower than the fast region (time [latex]400[/latex] to time [latex]800[/latex]) is fast. They don’t exactly cancel, so likely the train won’t quite reach [latex]22.6[/latex] km. Somehow, instead, we need to take into account the speed of the train at every instant. Sound familiar? This is where an integral is going to come it. Basically if we take the speed of the train at a small time frame, and multiply by the time it is going that speed, you get a picture that looks like this:

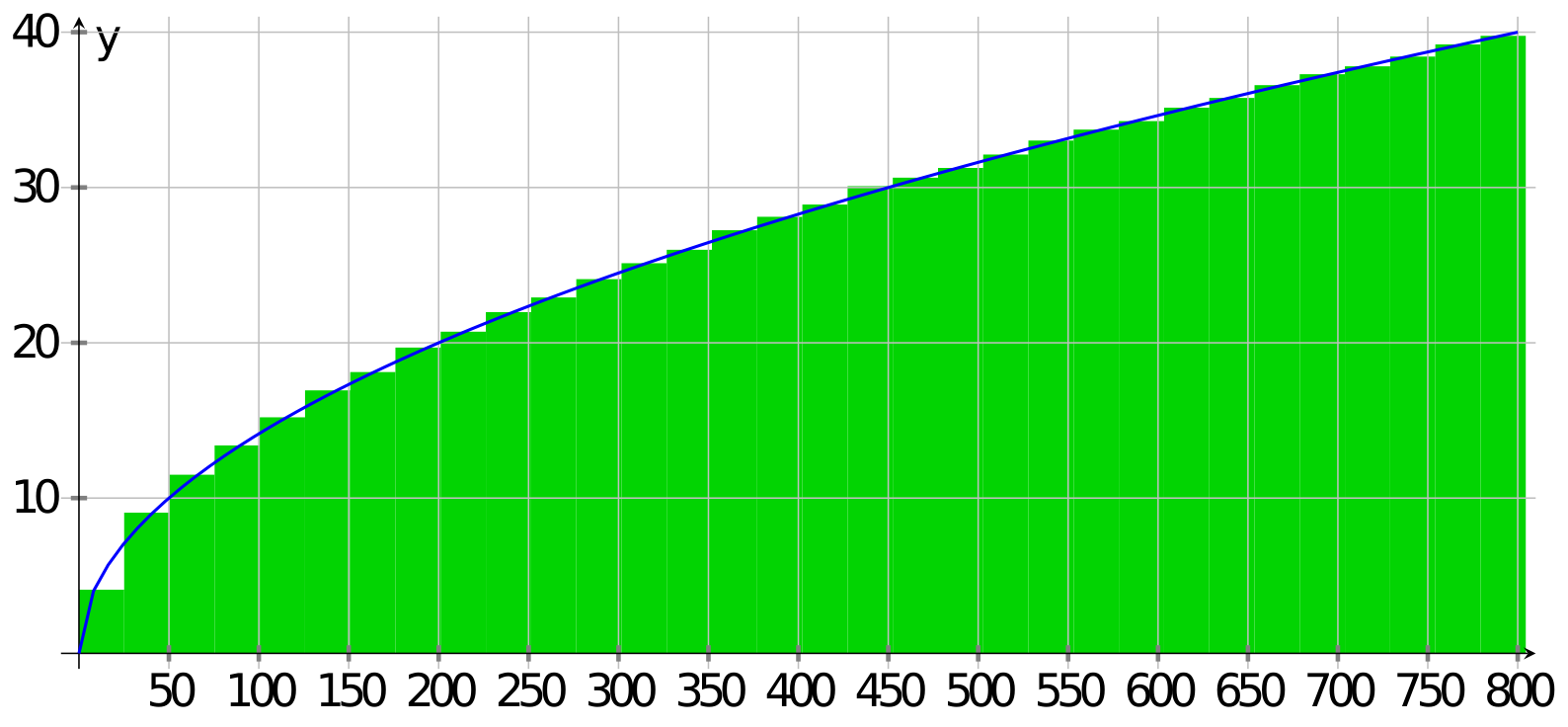
This is of course just the area under the curve! So we use the fundamental theorem of calculus to find the actual answer:
\begin{align*}
\int_0^{800} \sqrt{2t}dt & = \int_0^{800} \sqrt{2} \cdot \sqrt{t}dt \\
& = \int_0^{800} \sqrt{2} \cdot t^{1/2}dt \\
& = \sqrt{2} \cdot \frac{1}{3/2} \cdot t^{3/2} \bigg\rvert_{0}^{800} \\
& = \sqrt{2} \frac{1}{3/2} (800)^{3/2} – \sqrt{2} \frac{1}{3/2} (0)^{3/2} \\
& \approx 21300 \text{ m}
\end{align*}
A quick check to see if this is reasonable: we’re saying the train went 21.3 km in those 13 minutes. Seems a bit fast for a train but not impossible. It’s less than our max of 32 km, but more than the guess of 16 km that we thought it would beat. Seems reasonable!