Abstract

Digitale Interaktive Mathematische Maps_pdf

Defragmentierung als Antwort auf das Problem der doppelten Diskontinuität

Dem Übergang von der Schule zur Hochschule wird in der Literatur aller Fachrichtungen und Länder viel Aufmerksamkeit geschenkt. Grund hierfür sind nicht zuletzt die hohen Studienabbruchquoten von Studierenden in den ersten Semestern. Ein genauerer Blick auf die Studienabbruchquoten offenbart, dass diese in Studiengängen, in denen in den ersten Semestern Mathematikkurse belegt werden müssen, besonders hoch sind (Heublein 2014, Heublein und Schmelzer, 2018). Das hat dazu geführt, dass sich die mathematikdidaktische Forschung bezüglich der Übergangsproblematik meist auf die kognitiven Herausforderungen des Studiums, die sich aus den inhärenten Eigenschaften der Mathematik ergeben, konzentriert (vgl. z.B. Thomas et al., 2015). Insbesondere in der Lehrerbildung hat diese Perspektive eine lange Tradition. Bereits vor ca. 100 Jahren prägte der Mathematiker Felix Klein (1924/2016) den Begriff der „doppelten Diskontinuität“, um Probleme angehender Lehrerinnen und Lehrer beim Übergang von der Schule zur Hochschule und beim Übergang von der Hochschule zurück in die Schule zu thematisieren. Dazu schreibt er:

Der junge Student sieht sich am Beginn seines Studiums vor Probleme gestellt, die ihn in keinem Punkte mehr an die Dinge erinnern, mit denen er sich auf der Schule beschäftigt hat; natürlich vergi[ss]t er daher alle diese Sachen rasch und gründlich. Tritt er aber nach Absolvierung des Studiums ins Lehramt über, so soll er plötzlich eben diese herkömmliche Elementarmathematik schulmäßig unterrichten; da er diese Aufgabe kaum selbstständig, mit seiner Hochschulmathematik in Zusammenhang bringen kann, so wird er in den meisten Fällen recht bald die althergebrachte Unterrichtstradition aufnehmen, und das Hochschulstudium bleibt ihm nur eine mehr oder minder angenehme Erinnerung, die auf seinen Unterricht keinen Einflu[ss] hat. (Klein, 1924/2016, S. 1)

Den Grund für das Problem der doppelten Diskontinuität, die zweifelsohne ihren Beitrag zu den hohen Abbruchquoten leistet, sieht Klein also in der Fragmentierung von Schul- und Hochschulmathematik, deren Ursprung in der Verschiedenheit des Erscheinungsbildes der Mathematik in Schule und Universität liegt. Der Mathematikdidaktiker David Tall (2008) geht sogar so weit und beschreibt die Schul- und Hochschulmathematik als verschiedene Welten („worlds of mathematics“), indem er der anschaulich-symbolischen Mathematik der Schule die formal-axiomatische Mathematik der Hochschule gegenüberstellt. Letztendlich bringt dies auch eine Fragmentierung von Fachmathematik und Fachdidaktik mit sich, die didaktische Innovation und qualitativ hochwertigen Unterricht behindern. Natürlich ist es das Ziel der universitären Lehrerausbildung, dass behandelte fachmathematische Inhalte für den zukünftigen Unterricht in der Schule gewinnbringend eingesetzt werden können. Dies droht als Konsequenz der doppelten Diskontinuität zu scheitern. Untersuchungen von Winsløw und Grønbæk (2013) zeigen beispielsweise, dass Studierende nicht von sich aus in der Lage sind, Verbindungen zwischen Schul- und Hochschulmathematik herzustellen und dass der Transfer von universitären Inhalten in den schulischen Kontext nicht automatisch gelingt.

Um Kleins „doppelte Diskontinuität“ zu überwinden, müssen Studierenden Zusammenhänge zwischen der axiomatisch-formalen Welt der Hochschulmathematik und der anschaulich-symbolischen Welt der Schulmathematik aufgezeigt werden (vgl. Tall, 2008; Winsløw & Grønbæk, 2014). Dadurch rücken auch Fachwissenschaft und Fachdidaktik näher zusammen. Zum Zwecke der Defragmentierung von Fachwissenschaft und Fachdidaktik wurde im Teilvorhaben Mathematik das digitale Lernwerkzeug Digitale Interaktive Mathematische Maps (Brandl, 2009; dort: Interaktive Mathematische Landkarten) entwickelt und evaluiert^[1]. Konkretes Ziel der beteiligten Professuren (Didaktik der Mathematik und Reine Mathematik) ist vor allem das Aufzeigen von innermathematischen Zusammenhängen, sodass Inhalte aus den Fachveranstaltungen für die Didaktik der Mathematik und damit für den späteren Unterricht in der Schule nutzbar gemacht werden können.

Das Konzept der Digitalen Interaktiven Mathematischen Maps

In dem Artikel „The vibrating string – an initial problem for modern mathematics; historical and didactical aspects“ zeigt Brandl (2009) am Beispiel der schwingenden Saite eines Musikinstruments auf, dass wichtige mathematische Fragestellungen der Gegenwart meist eine lange Entwicklungsgeschichte aufweisen. Diese soll aus didaktischer Perspektive nutzbar gemacht werden, sodass sowohl die Rahmenbedingungen der Entwicklung als Kontextinformationen als auch der (mathematische) Entwicklungsprozess als Verständnishilfe in den Lernprozess miteinbezogen werden sollen.

Die konkrete Darstellung einer solchen Entwicklung sieht Brandl (2009) in einem didaktischen Tool, einer Art dreidimensionalem Baum oder Netz, in dem mathematische Inhalte als Knoten dargestellt werden, die mit Kanten verbunden werden. Das didaktische Tool visualisiert, dass mathematische Konzepte über einen langen Zeitraum hinweg und angestoßen von einem ursprünglichen mathematischen Problem/Inhalt entwickelt wurden (siehe Abbildung 1). Die ursprüngliche Idee von Brandl (2009) hat insgesamt eher die Problemgeschichte einzelner Inhalte im Blick, ist darauf aber keineswegs beschränkt und lässt sich auch auf ganze mathematische Teilgebiete oder die gesamte Mathematik übertragen.

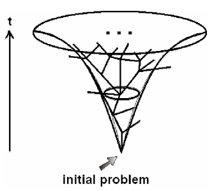
Brandl (2009) sieht in dem didaktischen Tool vor allem folgende Vorteile:

• Es visualisiert drei Dimensionen: Zeit in einer Dimension und in zwei Dimensionen thematische Ähnlichkeit.
• Es bietet eine ideale Transparenz der Zusammenhänge.
• Die einzelnen Knoten können verlinkt und mit Inhalten befüllt werden.
• Eine Zoom-Funktion kann ein tieferes Eintauchen in den Zusammenhang mathematischer Inhalte ermöglichen.
• Die mathematische Map erlaubt Horizontale und Vertikale Schnitte.

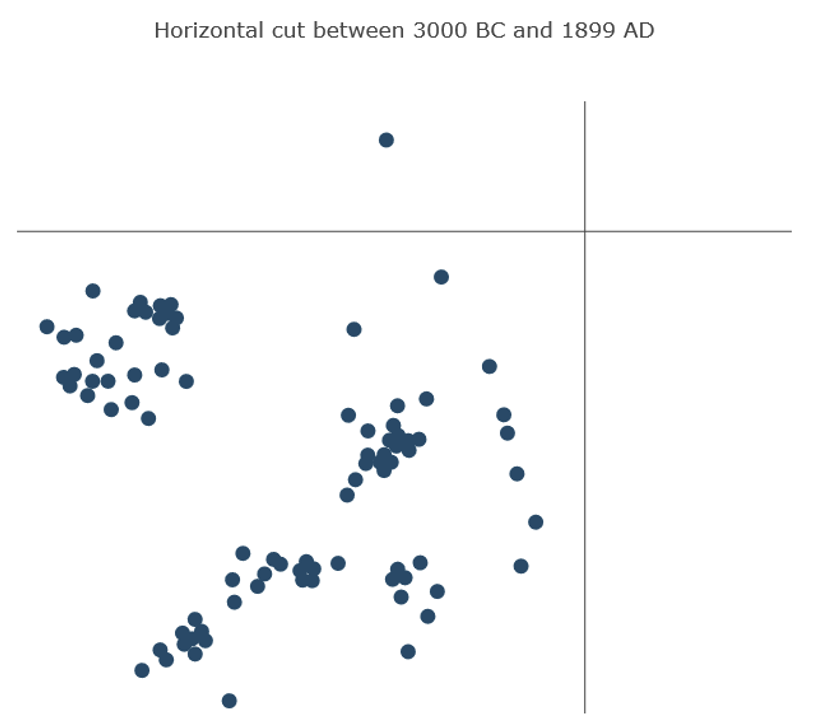
Als Zusatzfunktionen zur dreidimensionalen Darstellung sollen Horizontale und Vertikale Schnitte die Informationsentnahme erleichtern. Im Horizontalen Schnitt stehen dabei sogenannte historische Schichten im Mittelpunkt. Der Nutzer soll in die Lage versetzt werden, sich die sich entwickelnden mathematischen Konzepte eines Zeitpunktes oder einer Zeitspanne anzusehen, um einen Überblick über die thematische Verteilung der Inhalte zu dieser Zeit zu erlangen (siehe Abbildung 2).

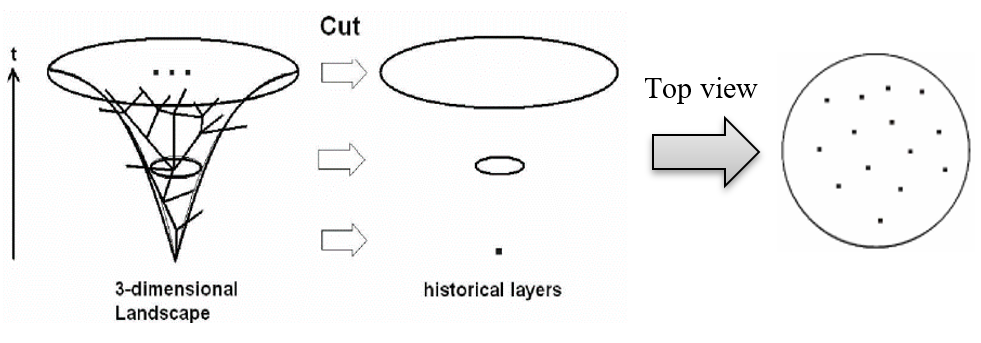
Im Vertikalen Schnitt hingegen geht es um die (isolierte) zweidimensionale Darstellung der historisch-zeitlichen Genese und der innermathematischen Entwicklungsschritte eines Inhaltes oder Teilgebietes (siehe Abbildung 3). Bei der konkreten Umsetzung wird deutlich, dass auf diese Art und Weise Schul- und Hochschulinhalte miteinander verknüpft werden können. Die anschaulichen und intuitiv mehr zugänglichen Schulinhalte sind häufig Meilensteine in der Entwicklung der abstrakten und formalen Hochschulinhalte.

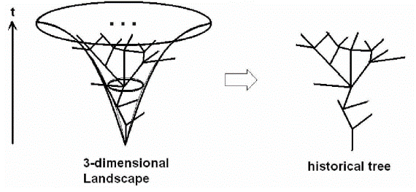
Im Drittmittelprojekt SKILL.de und hier im Teilvorhaben Mathematik ist das Konzept von Brandl implementiert worden. Es sind Digitale Interaktive Mathematische Maps für die Teilgebiete Geometrie, Algebra und Analysis entstanden. Nachfolgend soll das digitale Learningtool samt seiner Entwicklung dargestellt werden.

Design-based Research Methoden als Kombination von Entwicklung, Forschung und Lehre

Als günstiger Ansatz zur Entwicklung der digitalen mathematischen Maps haben sich design-based research-Methoden (vgl. Bakker, 2018) erwiesen. Sie können als „practical research methodology that could effectively bridge the chasm between research and practice in formal education” (Anderson & Shattuck, 2012, S. 16) beschrieben werden. Ausgehend von einem Blended Learning Kurs, der mithilfe der E-Learning-Plattform Ilias in der ersten Projektphase (Skill) implementiert wurde (siehe Datzmann & Brandl, 2019), konnte das Learningtool schließlich über mehrere Forschungszyklen hinweg entwickelt und verbessert werden. In Abbildung 4 (als reduzierter Darstellung der Fig. 2 in Przybilla et al., 2022) wird der Entwicklungsprozess schematisch dargestellt. Ein Forschungszyklus besteht dabei aus dem (Re-)Design des digitalen Tools, sowie der anschließenden Umsetzung/Implementation samt abschließender Evaluation, beides meist innerhalb eines universitären Mathematik- oder Didaktikkurses. Die abschließende Evaluation liefert dann Anregungen für die Weiterentwicklung (Re-Design) des betrachteten digitalen Learningtools. Im Folgenden sollen einige anfängliche Forschungs- und Designzyklen kurz skizziert werden, bevor exemplarisch ein zentraler Zyklus detaillierter dargestellt wird.

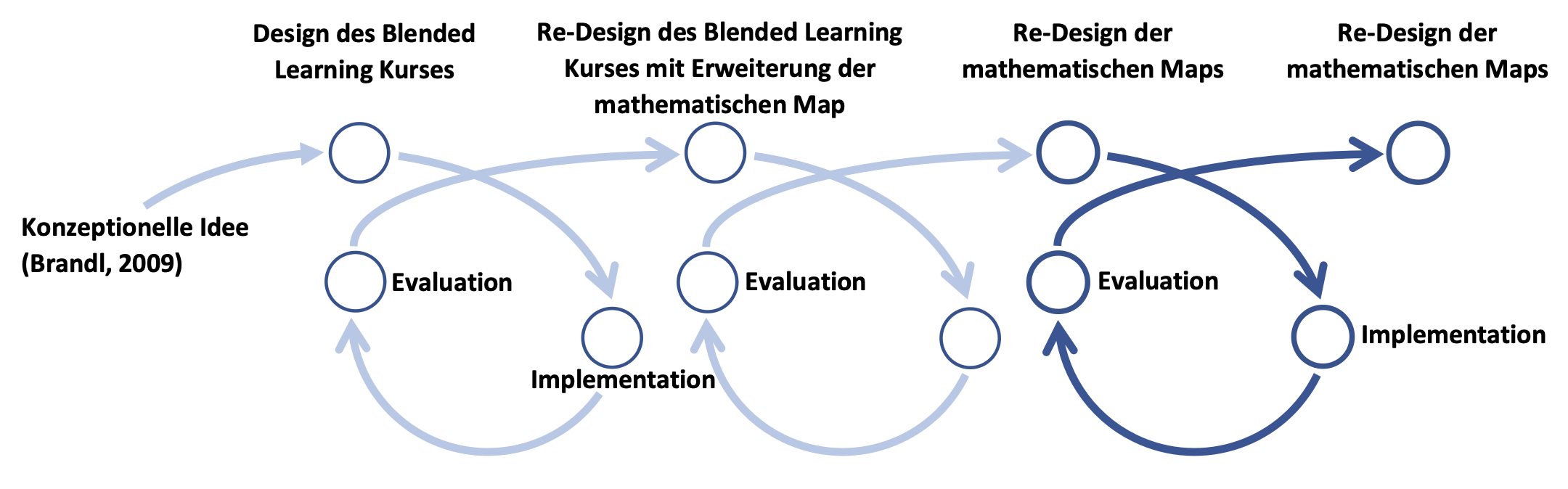
Beschreibung des Entwicklungsprozesses

In einem ersten Versuch, die mathematischen Maps zu implementieren, wurde die Programmiersprache Java-Skript verwendet, um einen dreidimensionalen Graphen zu erzeugen, in dessen Knoten mathematische Inhalte hinterlegt waren (vgl. Schwarz et al., 2017; siehe Abbildung 5). Aufgrund von Schwierigkeiten bei der Umsetzung wurde letztlich anstelle von mathematischen Maps eine Zeitleiste (Timeline) mit Meilensteilen der Entwicklung der Geometrie erstellt und verwendet (siehe Abbildung 6), die als Zusatzangebot auch in der aktuellen Map immer noch genutzt werden kann. In der Evaluation wurde der Schwerpunkt auf das Lehrformat an sich und weniger auf die Timeline gelegt, sodass die Ergebnisse hier weniger interessant sind (vgl. Datzmann & Brandl, 2019).

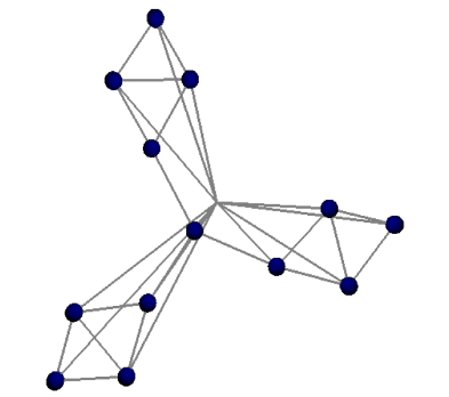
Anschließend wurden die mathematischen Maps entsprechend der ursprünglichen Designidee (Brandl, 2009) neugestaltet und in das verbesserte Lehrformat integriert. Die studentische Evaluation in diesem Zyklus hatte erneut einen starken Fokus auf das Blended-Learning Format (vgl. Datzmann et al., 2020), sodass das hier vorgestellte digitale Learningtool lediglich von einigen Fakultätsmitgliedern gezielt evaluiert und für den aktuellen Forschungszyklus leicht modifiziert wurde.

Detaillierte Beschreibung des aktuellen Forschungszyklus

Insgesamt war allerdings eine größere Nutzergruppe notwendig, um aussagekräftige Ergebnisse und Verbesserungsvorschläge zum digitalen Learningtool zu erhalten. Dies war durch die Kooperation mit der Karlstads Universitet in Schweden möglich. Dort wurde die Map als didaktisches Learningtool in einem Geometriekurs in der Ausbildung und Weiterbildung von Lehrern eingesetzt. Der aktuelle Zyklus wird nachfolgend genauer beschrieben.

Re-Design der mathematischen Maps als Ausgangspunkt des Forschungszyklus

Die interaktive dreidimensionale mathematische Map basiert auf einer konstruktivistischen Sichtweise des Lernens und soll „dem Lernenden eine optimale Lösung zum Aufbau erfolgreicher Lernprozesse bieten“ (Brandl, 2009, S. 106; übersetzt von den Autoren). Mathematische Inhalte sollen miteinander verknüpft, auf verschiedene Art und Weise präsentiert und eingebettet im historischen Kontext der Entdeckung präsentiert werden, damit möglichst viele Anknüpfungspunkte in den vorhandenen Wissensstrukturen gefunden werden (vgl. Wood et al., 1976). In der Map stellen die Knoten im Raum mathematische Inhalte dar. Mit Linksklick auf einen solchen Knoten öffnet sich eine Vorschau der hinterlegten Inhalte (siehe Abbildung 7). Für jeden Knoten wurde versucht, neben Informationen zum eigentlichen mathematischen Konzept auch Informationen zum Entdecker/Erfinder des mathematischen Inhalts, zum Kontext der Entdeckung, zu innermathematischen Zusammenhängen und zur Anwendung des Inhalts zu hinterlegen. Die Informationen sind dabei sowohl als Kurzbeschreibungen, als auch als Webpages oder Videos verlinkt, sodass man im Optimalfall zwischen mehreren Quellen und Medien wählen kann.

Die Kanten in der dreidimensionalen Map symbolisieren historische Entwicklungslinien, die Mathematik als eine sich entwickelnde Wissenschaft hervorheben (vgl. Schorcht, 2018). Felix Klein (1924/2016) würde die Vorgehensweise, die historische Entwicklung in den Lehrprozess miteinzubeziehen, als „anschaulich und genetisch kennzeichnen, d. h. das ganze Lehrgebäude wird auf Grund bekannter anschaulicher Dinge ganz allmählich von unten an aufgebaut“ und fügt an: „hierin liegt ein scharf ausgeprägter Gegensatz gegen den meist auf den Hochschulen üblichen logischen und systematischen Unterrichtsbetrieb“ (1924/2016, S. 6). Um die historischen und innermathematischen Zusammenhänge auch im Detail erforschen zu können, bietet die Benutzeroberfläche die Möglichkeit, die Map zu rotieren, hineinzuzoomen oder durch eine Filterfunktion nur bestimmte Knoten anzeigen zu lassen.

Das digitale Tool nutzt also die vertikale Dimension und die Entwicklungslinien, um eine historisch-genetische Sequenz zu visualisieren. Um zusätzlich einen Einblick in die Gleichartigkeit von mathematischen Inhalten und Konzepten zu geben, werden die verbleibenden zwei Dimensionen für die Darstellung der thematischen Ähnlichkeit verwendet. Der Blick von oben (siehe Abbildung 8) lässt erahnen, dass die Knoten nicht zufällig in der Ebene verteilt, sondern thematisch geclustert sind. Ziel der Darstellung ist es, dass über den euklidischen Abstand Rückschlüsse auf die Ähnlichkeit von Knoten gezogen werden können. Das bedeutet, dass thematisch ähnliche Knoten näher beieinander und thematisch sehr verschiedene Knoten weiter voneinander entfernt liegen sollen. Die Anordnung der Knoten in der horizontalen Ebene wird über einen kräfte-basierten Algorithmus durchgeführt. Technische Details hierzu finden sich in Przybilla et al. (2021).

Ergänzende Funktionen der interaktiven mathematischen Map

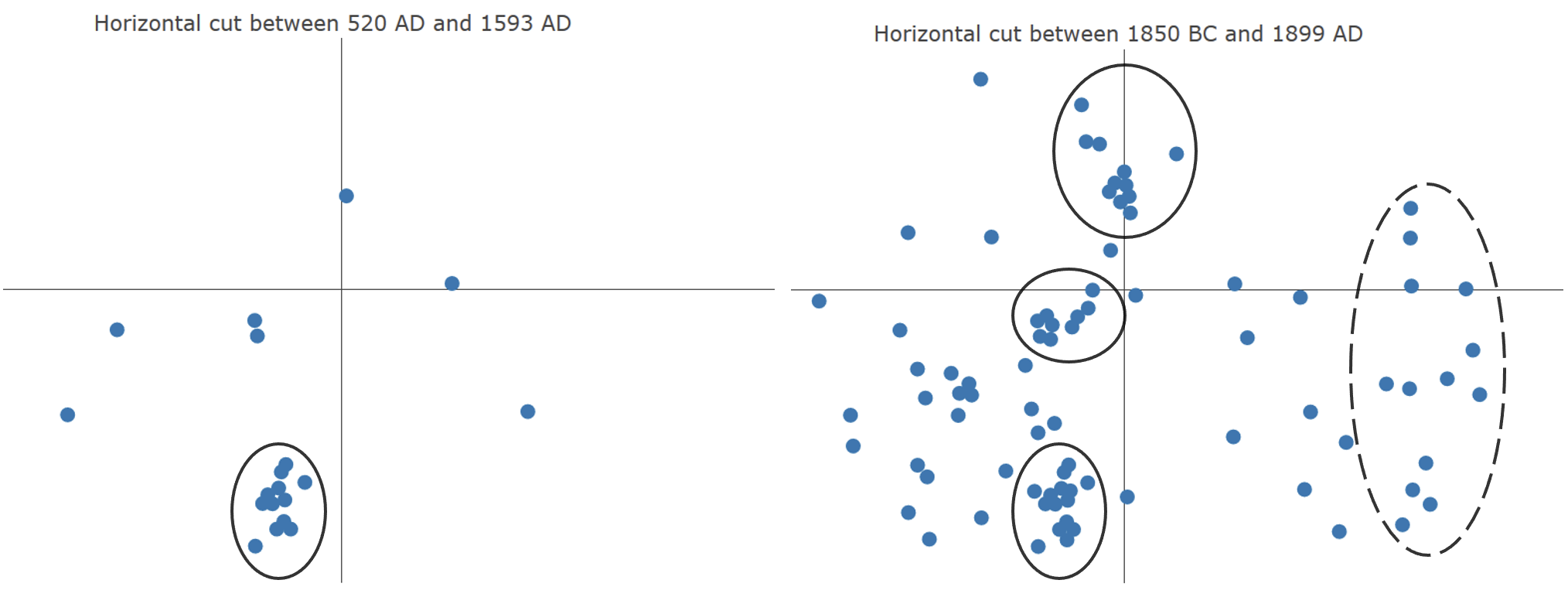
Informationen werden von unserem Gehirn auf Basis von thematischen Zusammenhängen und thematischer Ähnlichkeit gebündelt (vgl. Hoffmann & Engelkamp, 2017, S. 143-147). Das Design der mathematischen Maps orientiert sich an dieser Eigenschaft unseres Wissenssystems und nutzt zwei Dimensionen, um die thematische Beziehung über die euklidische Distanz auszudrücken. Um das Erkennen ähnlicher Inhalte zu erleichtern, bietet das digitale Tool die Möglichkeit, „Horizontale Cuts“ (Brandl, 2009) einzusetzen. Diese Funktion projiziert alle Knoten in eine Ebene, sodass die thematische Ähnlichkeit der verschiedenen Inhalte sichtbar wird. Abbildung 9 links zeigt den Horizontalen Cut für das Zeitintervall von 520 n. Chr. bis 1593 n. Chr in der Geometrie-Map. Die Ellipse markiert Inhalte zum Thema Trigonometrie, die von arabischen Mathematikern entdeckt wurden. Ansonsten wurde in diesem Zeitraum wenig entwickelt. Betrachtet man den Horizontalen Schnitt von 1850 v. Chr. bis 1899 n. Chr. rechts, so werden auch hier ähnliche Inhalte als gebündelt erkennbar (manuell durch Ellipsen hervorgehoben). Hier wird außerdem die zunehmende Ausdifferenzierung der Mathematik im Laufe der Zeit sichtbar. Die gestrichelte Ellipse markiert Inhalte der nicht-euklidischen Geometrie, die vor allem im 18. und 19. Jahrhundert entdeckt bzw. entwickelt wurden. Die Knotenpunkte auf der linken Seite stellen eher elementare geometrische Inhalte dar, von denen man zahlreiche auch in der Schule wiederfindet. Wie in der dreidimensionalen Map können auch in den zweidimensionalen Darstellungen durch einen Klick die Inhalte der Knoten in einer Vorschau angezeigt werden.

Um das Verstehen neuer Inhalte zu erleichtern, empfiehlt es sich, komplexe Inhalte, wenn möglich, so darzustellen, dass sie als (historische) Weiterentwicklung von einfacheren, intuitiven und anschaulichen Inhalten erkennbar werden. Der deutsche Mathematiker Max Draeger beschreibt den Grundgedanken dieser Methode folgendermaßen:

Ein formales Verstehen… ist dem logisch geschulten Geiste wohl möglich. Das in die Sache eindringende Begreifen ist es ohne die Kenntnis der Geschichte nicht. Im Gegenteil begünstigt die Isolierung von der historischen Entwicklung leicht Mi[ss]deutungen…, die schließlich zu irrigen Mathematikauffassungen führen. (Draeger, 2012, S. 10).

Die Isolation der Mathematik von ihren Wurzeln kann also zu einem falschen Verständnis von Mathematik führen, was in jedem Fall vermieden werden muss. Um die historische Entwicklung mathematischer Konzepte deutlich zu machen, wird die Funktionalität „Vertikaler Cut“ (Brandl, 2009) angeboten. Durch die Auswahl eines gewünschten Knotens öffnet sich ein neues Fenster, in dem dieser Knoten und alle historisch-genetisch zusammenhängenden Inhalte, die zur Entdeckung/Entwicklung dieses Inhalts geführt haben, inklusive ihrer Entwicklungslinien, in einer zweidimensionalen Darstellung dargestellt werden (siehe Abbildung 10). Dadurch kann die historische Genese eines Inhalts nachvollzogen werden.

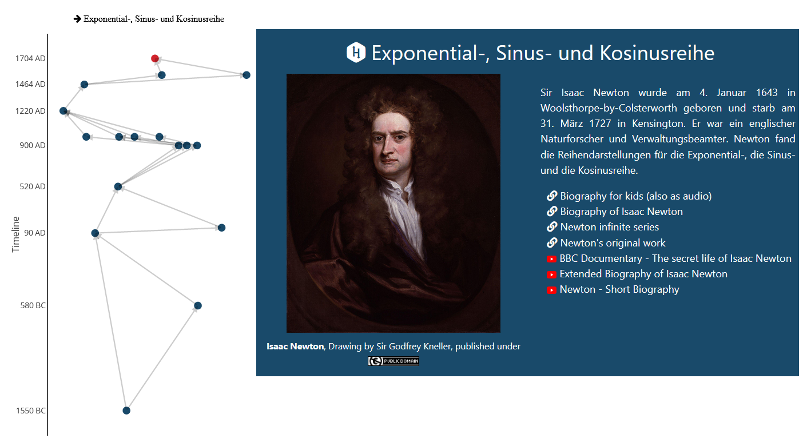
Der abgebildete Vertikale Cut zeigt die Entwicklung der Trigonometrie ausgehend von ihren Anfängen, als die Ägypter mit ihr elementare Berechnungen zur Steigung von Pyramiden durchführten. Über die aus der Schule bekannten Strahlensätze von Thales entwickelten die arabischen Mathematiker die bis heute in den Gymnasien gelehrte Trigonometrie. Mit dem Aufkommen der analytischen Geometrie wurden Rahmenbedingungen geschaffen, unter denen Isaac Newton die komplexen analytischen Reihen trigonometrischer Funktionen, die heute an den Universitäten gelehrt werden, aufstellen konnte. Auf der linken Seite von Tabelle 1 werden nochmals im Detail wichtige Entwicklungsstufen auf dem Weg zur universitären Trigonometrie zusammengefasst, während auf der rechten Seite der entsprechende Vertikale Cut abgebildet ist. An dieser Stelle wird deutlich sichtbar, wie das Learningtool dazu beitragen kann, dass Schul- und Hochschulinhalte als verknüpft wahrgenommen werden. Im historischen Rückblick wird sichtbar, dass sich Hochschulinhalte häufig aus den aus der Schule bekannten Inhalten entwickelt haben. Auf diese Art und Weise können Hochschulinhalte als Weiterentwicklung, Abstraktion oder Verallgemeinerung der Schulinhalte verstanden werden.

Sowohl im Vertikalen als auch im Horizontalen Schnitt gibt es verschiedene Zusatzfunktionen, die über eingeblendete Buttons ausgeführt werden können. Beispielsweise bietet ein Button die Möglichkeit, eine Internetseite zu erstellen, auf der alle sichtbaren Knoten samt ihren Inhalten in chronologischer Reihenfolge sortiert abgebildet werden. Hiermit lassen sich beispielsweise alle Inhalte der Knoten eines Vertikalen Schnittes bequem einsehen, sodass die historische Entwicklung einfach nachvollzogen werden kann. Zudem können die so erstellten Internetseiten heruntergeladen werden und dann auch offline geöffnet und mit anderen Nutzern geteilt werden.

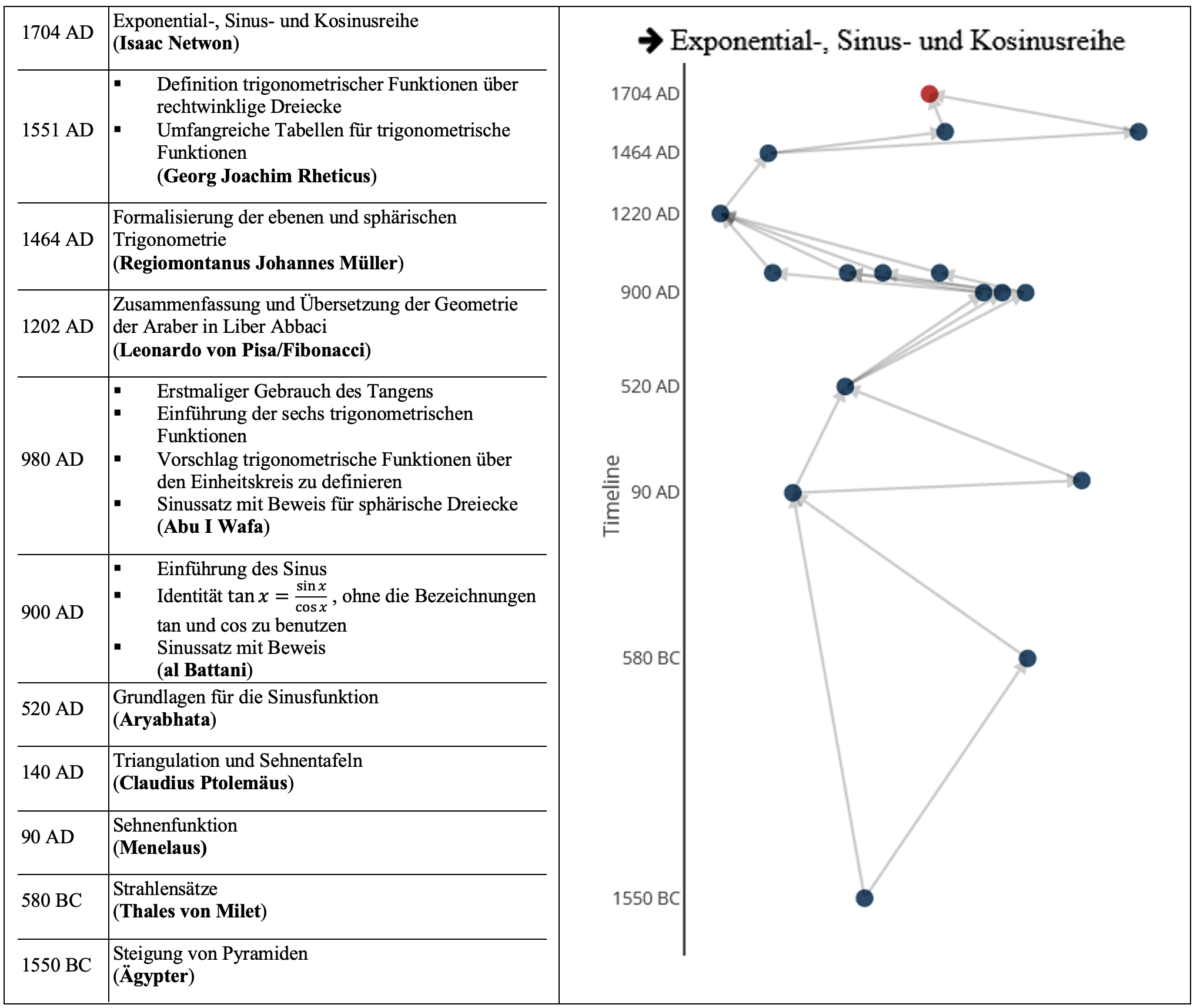
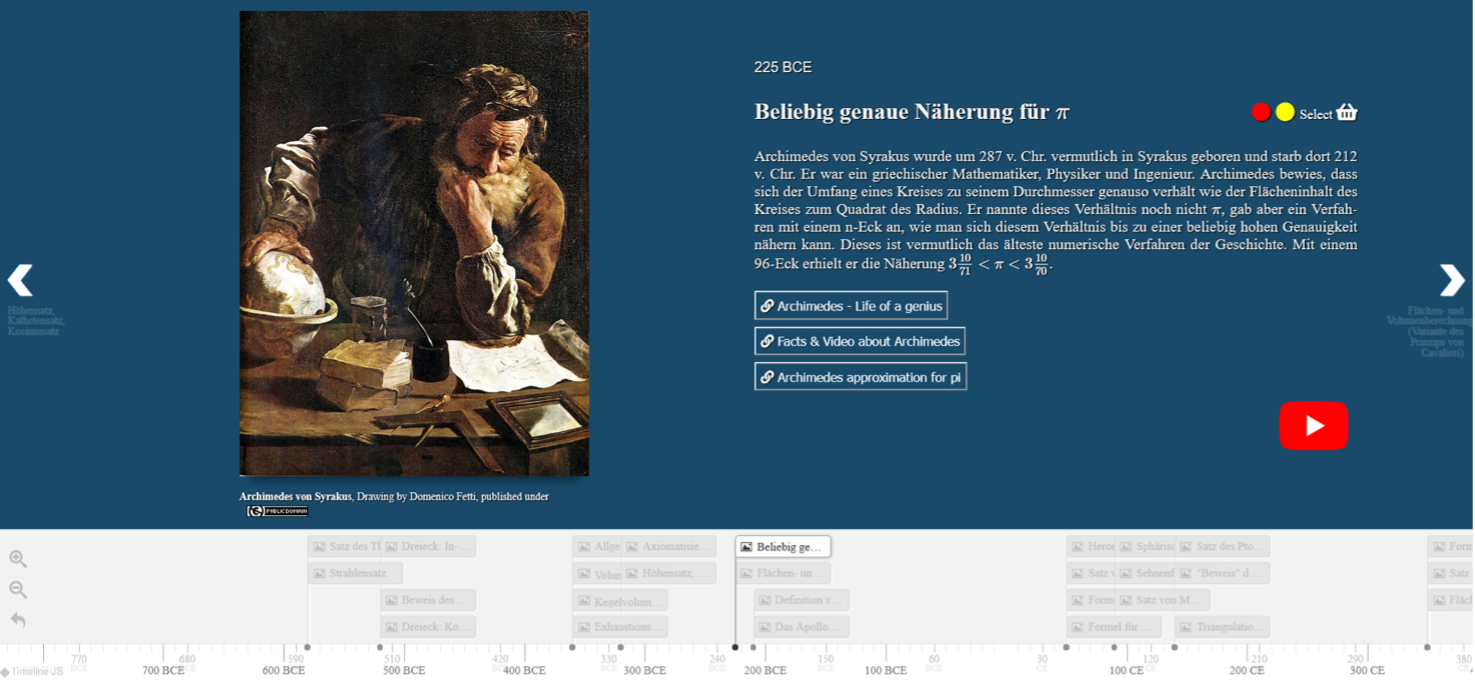
Während die bisher dargestellten Beispiele aus dem Gebiet der Geometrie stammen, wurden auch weitere Maps zur Algebra und Analysis entwickelt. Es ist geplant, diese durch zusätzliche Maps zu weiteren Teilgebieten der Mathematik zu ergänzen. Wie die vorherigen Abbildungen zeigen, gibt es die Möglichkeit, zwischen einer Version mit den erläuternden Texten auf deutsch (vgl. z.B. Abbildung 6) und einer Version mit englischen Texten (vgl. z.B. Abbildung 7) zu wechseln. Bei den Links zu Texten aus dem Internet oder YouTube-Videos wird jeweils angegeben^[2], in welcher Sprache der Text bzw. das Video vorliegt (vgl. Abbildung 11).

Implementation/Einsatz der Maps als digitales Learningtool

Im beschriebenen Forschungszyklus wurde die öffentlich zugängliche mathematische Map für Geometrie als Teil eines Mathematikkurses an der Karlstads Universitet in Schweden verwendet^[3]. Der Kurs ist im zweiten Semester des Lehramtsstudiums verankert und kann auch von Lehrkräften besucht werden, die sich mathematisch weiterbilden möchten. Die einzelnen Komponenten des Kurses wurden gemeinsam von Fachwissenschaftlerinnen und Fachwissenschaftlern und Fachdidaktikerinnen und Fachdidaktikern der Karlstad Universitet und der Universität Passau konzipiert. Inhaltliches Ziel des Kurses ist es, zentrale Inhalte der euklidischen Geometrie zu vermitteln und Schlüsselkonzepte der nichteuklidischen Geometrie einzuführen. Darüber hinaus fordert der Modulkatalog die Förderung der Entwicklung von Kompetenzen zur Bewertung digitaler Lehr- und Lernwerkzeuge. Im betrachteten Semester haben 44 (von insgesamt 64) Studierenden (27 Lehrkräfte, 17 Lehramtsstudierende) aktiv an der Lehrveranstaltung teilgenommen. Die wöchentlichen Vorlesungen wurden durch Inhalte und Arbeitsaufträge ergänzt, die sich mit der digitalen mathematischen Map befassten, sodass anschließend eine Evaluation der einzelnen Komponenten des digitalen Tools stattfinden konnte. Aufgrund der zeitlichen Beschränkungen im Studienplan wurde dies in wöchentliche kurze Abschnitte aufgeteilt. Die Arbeitsaufträge waren chronologisch wie folgt angeordnet:

1. Timeline (TL)
2. Narrative Didaktik als Anwendungsbereich der Inhalte der mathematischen Map
   (vgl. Brandl, 2017)
3. Dreidimensionale mathematische Map (3D Map)
4. Vertikaler Cut (VC)
5. Horizontaler Cut (HC)
6. Anwendungsaufgabe: Die Diskussion um das Parallelenaxiom
7. Abschließende und allgemeine Bewertung der mathematischen Map für den eigenen Lernprozess, sowie Bewertung des Potenzials für das Lehren an Schulen

Jede Woche konnten die Studierenden einen Teil der Map angeleitet kennenlernen. Hierfür wurden kurze Demonstrationsvideos erstellt. Anschließend hatten die Teilnehmenden die Aufgabe, die jeweilige Funktionalität an einem Arbeitsauftrag selbst auszuprobieren.

Evaluation der Digitalen Interaktiven Mathematischen Maps

In wöchentlichem Turnus erfolgte die technische und inhaltliche Evaluation der Map mittels eines Quiz (Format: Single-Choice-Fragen mit 5-stufiger Likert-Skala als Antwortmöglichkeit sowie Fragen mit freien Antwortmöglichkeiten) und der Möglichkeit für allgemeines Feedback hinsichtlich Anregungen oder Verbesserungsvorschlägen. Den Abschluss des Kurses bildete eine weitere Evaluation über den gesamten Verlauf. Hierbei war das Ziel, Rückschlüsse über den jeweiligen Lernzuwachs durch Verwendung der Map zu ziehen sowie die Verwendbarkeit im Schulunterricht zu beurteilen bzw. das Potential dafür einzuschätzen.

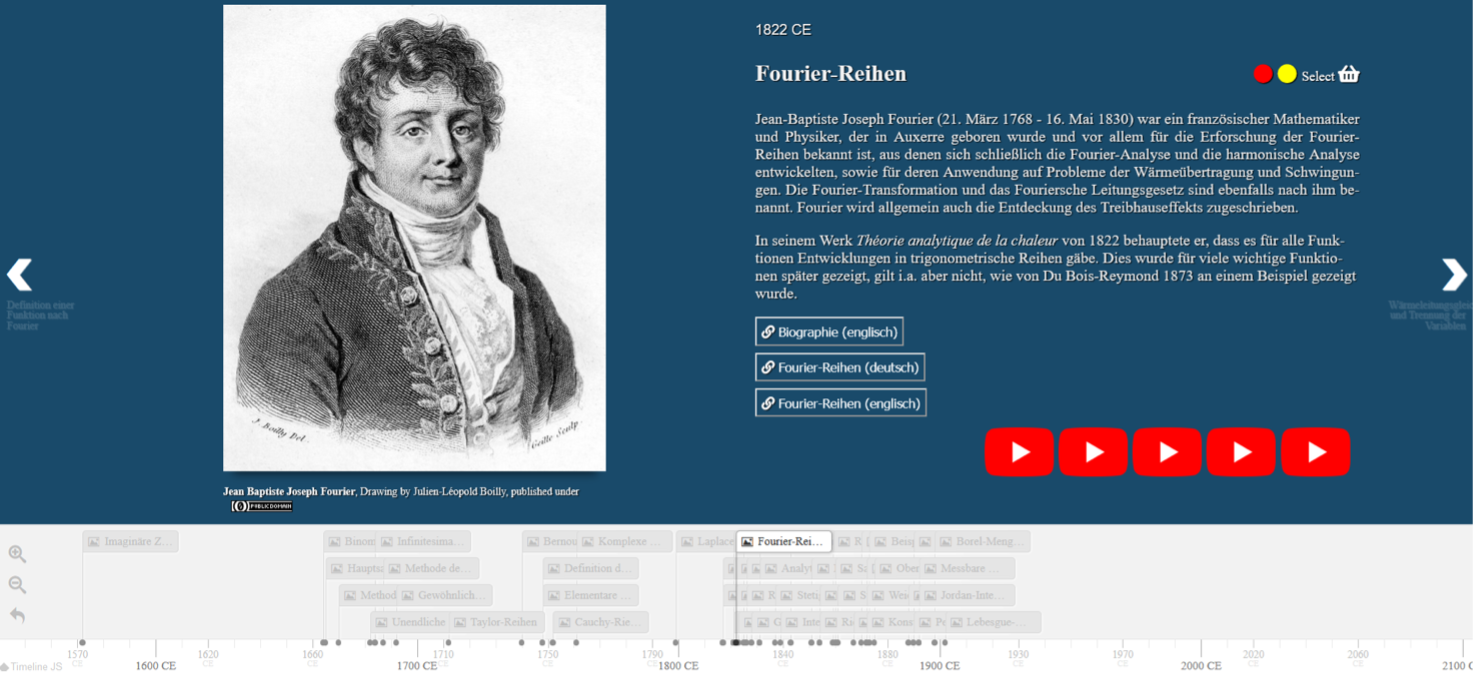
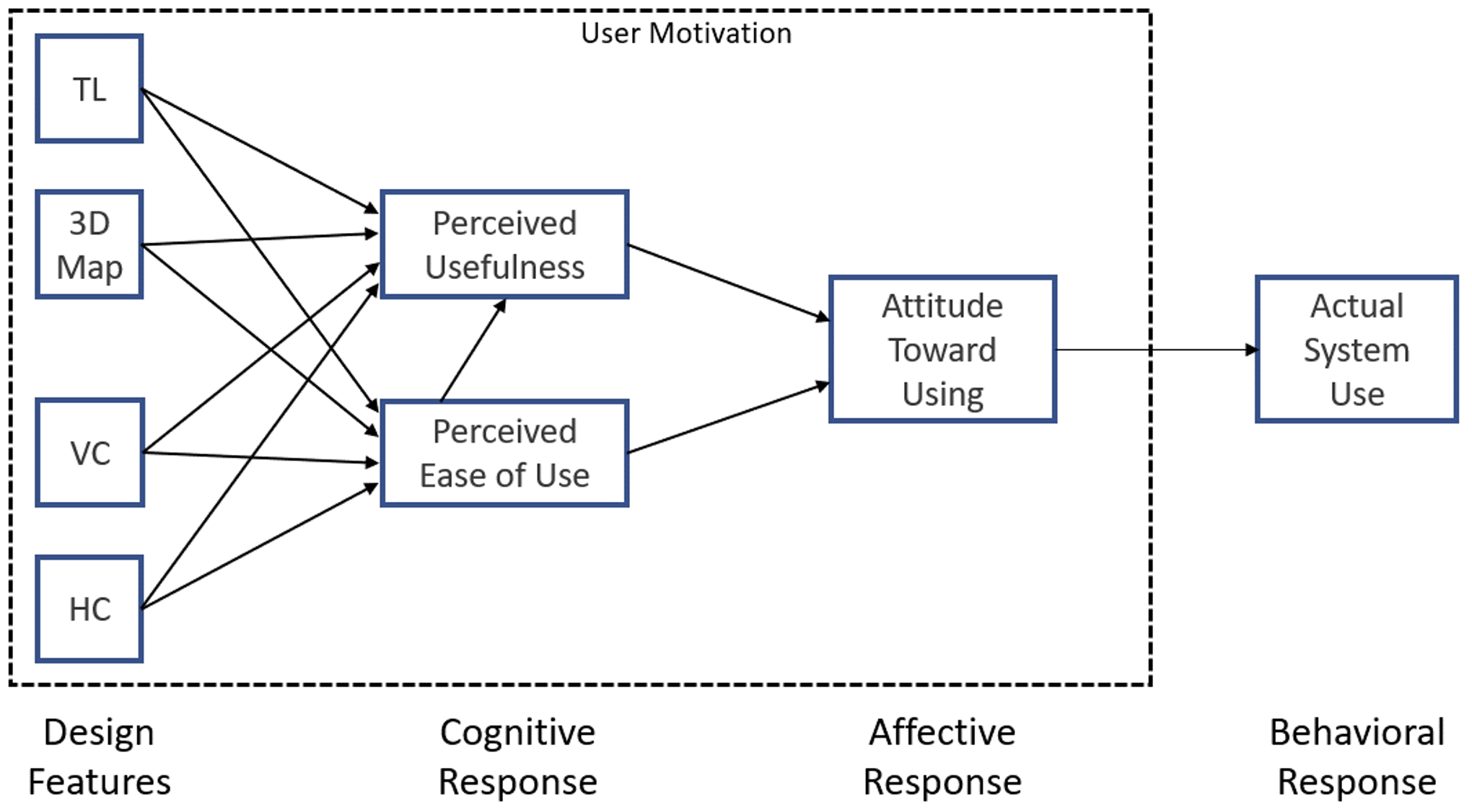
Als Grundlage für die technische Evaluation des digitalen Tools wurde das weit verbreitete Technology Acceptance Model von Davis (TAM, 1985; siehe Abbildung 12), das sowohl theoretisch als auch empirisch gut belegt ist (vgl. Scherer, Siddiq & Tondeur, 2019), verwendet (siehe auch Przybilla et al., 2022; Vinerean et al., in press).

According to the model, a potential user’s overall attitude toward using a given system is […] a major determinant of whether or not he actually uses it. Attitude toward using, in turn, is a function of two major beliefs: perceived usefulness and perceived ease of use. Perceived ease of use has a causal effect on perceived usefulness. Design features directly influence perceived usefulness and perceived ease of use. (Davis, 1985, p. 24)

Demnach sind die determinierenden Faktoren für den tatsächlichen Einsatz eines Tools die wahrgenommene Nützlichkeit und die wahrgenommene Benutzerfreundlichkeit. Diese wiederum hängen entscheidend von den Eigenschaften der Design-Features ab. In unserem Fall können die einzelnen Komponenten und Funktionalitäten der Map als Design-Features betrachtet werden (siehe Abbildung 11). In den Quizfragen wird nach der wahrgenommenen Benutzerfreundlichkeit und der wahrgenommenen Nützlichkeit (für das Lernen der Studierenden und die mögliche Nutzung in der Schule) der einzelnen Komponenten der Map gefragt. Darauf aufbauend können Rückschlüsse über die Benutzerfreundlichkeit und Nützlichkeit des gesamten digitalen Tools gezogen werden.

Aus didaktischer Sicht dient die Evaluation in diesem Forschungszyklus lediglich der offenen Generierung von Hypothesen zur Wirkung des digitalen Tools auf den Lernzuwachs der Studierenden. Die generierten Hypothesen können dann in dem darauffolgenden Forschungszyklus verifiziert oder falsifiziert werden.

Erkenntnisse aus der Evaluation

An dieser Stelle sollen einige Ergebnisse exemplarisch hervorgehoben werden, die bestätigen, dass die Map in ihrer derzeitigen technischen Umsetzung als durchaus nützlich und einfach zu bedienen wahrgenommen wurde. Der Fokus liegt hierbei auf technischen Elementen, die als Hinweise für Anpassungen im nächsten Forschungszyklus interpretierbar sind.

Generell gab es zahlreiche Vorschläge zur Verbesserung des didaktischen Tools, die in ihrer Häufigkeit und Tiefe zeigen, dass sich die Studierenden intensiv mit dem digitalen Tool und dessen Nutzen für Lehr- und Lernprozesse auseinandergesetzt haben. Damit scheint der Aufbau von Kompetenzen, wie im Modulkatalog gefordert, im Bereich der Evaluation von digitalen Lehr- und Lernwerkzeugen angestoßen.

Die Zeitleiste wurde von über 80% der Teilnehmenden als nützlich empfunden, um historische Ereignisse übersichtlich und strukturiert darzustellen. Ein Inhaltsverzeichnis oder eine Suchfunktion innerhalb der Zeitleiste wurden mehrfach gefordert, um einen klaren Überblick über die enthaltenen Inhalte zu erlangen. Dies könnte die Nützlichkeit der Timeline zusätzlich erhöhen. In der dreidimensionalen Map wurden sowohl die Such- als auch die Filterfunktion von 89% der aktiv Teilnehmenden als hilfreich bewertet. Auch die Vorschau innerhalb der Map wurde von fast 80% als hilfreich angesehen. Ein großer Teil der verbleibenden 20% störte sich an einem technischen Detail, das inzwischen angepasst wurde. Während nur eine Person angab, die Timeline sei schwierig zu bedienen, wurden beim Umgang mit der dreidimensionalen Map mehr Schwierigkeiten erwartet, sodass eine kurze Schulung für einen reibungslosen Umgang mit der Map als sinnvoll erachtet wurde. Dies sollte bei der Verwendung der Maps in anderen Settings auch berücksichtigt werden. Der Aussage „Ich halte die Funktion ‘Vertikaler Cut’ für eine nützliche und übersichtliche Möglichkeit, historische Entwicklungen darzustellen“ stimmten 95% der Teilnehmenden zu. Außerdem sahen die Studierenden und Lehrkräfte in dieser Funktionalität das größte Potential für den Einsatz des didaktischen Werkzeugs in der Schule. Der Horizontale Schnitt wurde von 93% als geeignetes Mittel angesehen, um innermathematische Zusammenhänge aufzuzeigen.

Aus didaktischer Sicht scheinen die Evaluationsergebnisse anzudeuten, dass der Einsatz der Map (innerhalb dieses Kurses) zu positiven Ansichten über das Wesen der Mathematik („favorable beliefs concerning the nature of mathematics“) beiträgt, „[which] are a crucial part of the professional competence of mathematics teachers“ (Felbrich et al., 2008, S. 763). In diesem Zusammenhang wird zwischen folgenden Orientierungen unterschieden (vgl. ebd., S. 764).:

• „the formal-related orientation“: Mathematik als exakte Wissenschaft, die auf Axiomen beruht und die davon durch logische Schlüsse abgeleitet wird,
• „the scheme-related orientation“: Mathematik als Sammlung von Ausdrücken, Regeln und Formeln, die dann eindeutig angewandt werden müssen,
• „the process-related orientation“: Mathematik als Wissenschaft, in der es um den Prozess des Problemlösens und der Entdeckung von Strukturen geht und
• „the application-related orientation“: Mathematik als Wissenschaft, die für das Leben und die Gesellschaft durch Anwendungen von Bedeutung ist.

Die ersten beiden Anschauungen vermitteln ein statisches und für Lehrende und Lernende ungünstiges Bild der Mathematik, das zudem mit der Darstellung von Mathematik im Lehrplan nicht kompatibel ist (vgl. ebd.; ISB, LehrplanPLUS Fachprofil Mathematik). Die letzten beiden Anschauungen hingegen spiegeln ein dynamisches Verständnis von Mathematik wider und betonen Mathematik als sich entwickelnde Wissenschaft, zu der Fehler naturgemäß dazugehören. Sie fördern eine akkurate und mit dem Lehrplan kompatible Sicht auf Mathematik und mathematisches Tun, sodass eine offene und damit für das Lernen günstige Fehlerkultur etabliert werden kann^[4].

Viele Antworten der Nutzerinnen und Nutzer der Map in diesem Forschungszyklus deuten auf eine prozess- und anwendungsorientierte Sicht auf Mathematik hin. Ein Teilnehmer schrieb beispielsweise, dass die Darstellung der Geschichte der Mathematik, wie sie durch die Map erfolgt, zeigt, „that mathematics is a subject that has been evolved over a long time and in close proximity to practical problems“.

Zusammenfassung

Der vorliegende Artikel zeigt anhand eines design-based research Ansatzes auf, wie die eigene Lehre für den Entwicklungsprozess eines digitalen Tools genutzt werden kann. Dabei wurden die Digitalen Interaktiven Mathematischen Maps sukzessive weiterentwickelt, sodass der aktuelle Stand der Map als Ergebnis eines langen Prozesses, in dem jeder Teilschritt als ein wertvoller Beitrag zum letztendlichen Ergebnis angesehen werden muss. Die aktuelle Evaluation deutet darauf hin, dass die technische Umsetzung des Ausgangskonzeptes gelungen ist. Die qualitative Auswertung der Freitextantworten der Evaluation legt außerdem die Hypothese nahe, dass durch den Einsatz der Map ein für Lehrkräfte günstiges und akkurates Bild von Mathematik als prozess- und anwendungsorientierte Wissenschaft gefördert werden kann.

Literatur

Anderson, T. & Shattuck, J. (2012). Design-based research: A decade of progress in education research? Educational Researcher, 41, 16–25.

Bakker, A. (2018). Design Research in Education. London, UK: Routledge.

Brandl, M. (2017). Narrative Didaktik als Vernetzungsinstrument: die Schule von Athen. In: T. Borys, M. Brandl, A. Brinkmann (Hrsg.). Mathe vernetzt – Anregungen und Materialien für einen vernetzenden Mathematikunterricht. Band 6. Schriftenreihe des GDM-Arbeitskreises ‚Vernetzungen im Mathematikunterricht’ (A. Brinkmann, Reihenherausgeberin),  Appelhülsen, Verlag Bücherbunt im MUED e.V., 7–20.

Brandl, M. (2016). Narrative Mathematik-Didaktik mittels Elementen bildender Kunst. In: Institut für Mathematik und Informatik der Pädagogischen Hochschule Heidelberg (Ed.), Beiträge zum Mathematikunterricht 2016. Münster: WTM-Verlag, 1415–1418.

Brandl, M. (2010). Narrative Didactics in Mathematical Education: an innovative Didactical Concept. In: T. Bianco & V. Ulm (Ed.): Mathematics Education with Technology – Experiences in Europe, Augsburg: University of Augsburg, 103–110.

Brandl, M. (2009). The vibrating string – an initial problem for modern mathematics; historical and didactical aspects. In: Witzke (Ed.): Mathematical Practice and Development throughout History: Proceedings of the 18th Novembertagung on the History, Philosophy and Didactics of Mathematics. Berlin: Logos Verlag, 95–114.

Datzmann, A., & Brandl, M. (2019). Evaluation of a connecting teaching format in teacher education. In: U. T. Jankvist et al. (Eds.), Proceedings of the Eleventh Congress of the European Society for Research in Mathematics Education (CERME 11, February 06–10, 2019) (pp. 2462–2463). Utrecht: Freudenthal Group & Freudenthal Institute, Utrecht University and ERME. https://hal.archives-ouvertes.fr/hal-02422599

Datzmann, A., Przybilla, J., Brandl, M., & Kaiser, T. (2020). New Teaching Techniques aiming to connect School and University Mathematics in Geometry. In: A. Donevska-Todorova, et al. (Eds.): Mathematics Education in the Digital Age (MEDA) PROCEEDINGS 2020 (pp. 37–44). Villeurbanne: HAL. https://hal.archives-ouvertes.fr/hal-03754749

Davis, F. D. (1985). A technology acceptance model for empirically testing new end-user information systems: Theory and results. (PhD), Massachusetts Institute of Technology, Cambridge, MA. http://hdl.handle.net/1721.1/15192

Draeger, M. (2012). Die Philosophie in der Mathematik: Geschichte der Mathematik im Überblick. Dresden: Uhlig Verlag.

Felbrich, A., Müller, C., & Blömeke, S. (2008). Epistomological Beliefs Concerning the Nature of Mathematics among Teacher Educators and Teacher Education Students in Mathematics. ZDM Mathematics Education, 40, 763–776. https://doi.org/10.1007/s11858-008-0153-5

Fraefel, U. (2014). Professionalization of pre-service teachers through university-school partnerships. Partner schools for Professional Development: development, implementation and evaluation of cooperative learning in schools and classes. Edinburgh: WERA Focal Meeting.

Gueudet, G., Bosch, M., diSessa, A., Kwon, O.-N., & Verschaffel, L. (2016). Transitions in mathematics education. Berlin: Springer.

Heublein, U., & Schmelzer, R. (2018). Die Entwicklung der Studienabbruchquoten an den deutschen Hochschulen. Hannover: DZHW.

Heublein, U. (2014). Student Drop-out from German Higher Education Institutions. European Journal of Education, 49(4), 497–513. https://doi.org/10.1111/ejed.12097

Hoffmann, J., & Engelkamp, J. (2017). Lern- und Gedächtnispsychologie [Learn- and Memo-rypsychology] (2nd ed.). Berlin, Saarbrücken: Springer.

Klein, F. (2016). Elementary Mathematics from higher standpoint. Volume I: Arithmetic Algebra Analysis. (G. Schubring, Trans.) Springer. [Original work published 1924]. https://doi.org/10.1007/978-3-662-49442-4

Przybilla, J., Brandl, M., Vinerean, M., & Liljekvist, Y. (2022). Digital mathematical maps – results from iterative research cycles. In J. Hodgen, E. Geraniou, G. Bolondi & F. Ferretti. (Eds.), Proceedings of the Twelfth Congress of the European Society for Research in Mathematics Education (CERME12) (pp.1-8). Free University of Bozen-Bolzano and ERME. https://hal.archives-ouvertes.fr/hal-03754749/

Przybilla, J., Brandl, M., Vinerean, M., & Liljekvist, Y. (2021). Interactive Mathematical Maps – A contextualized way of meaningful Learning. In: G. A. Nortvedt et al. (Eds.): Bringing Nordic mathematics education into the future. Preceedings of NORMA 20. The ninth Nordic Conference on Mathematics Education. Oslo, 2021 (pp. 209–216). Göteborg: SMDF. https://www.uv.uio.no/ils/english/about/events/2021/norma/proceedings/norma_20_preceedings.pdf

Scherer, R., Siddiq, F., & Tondeur, J. (2019). The technology acceptance model (TAM): A meta-analytic structural equation modeling approach to explaining teachers’ adoption of digital technology in education. Computers & Education, 128, 13–35. https://doi.org/10.1016/j.compedu.2018.09.009

Schorcht, S. (2018). Typisierung mathematikhistorischer Beispiele in deutschen Mathematikschulbüchern der Klassenstufen 1 bis 7. Münster: WTM-Verlag.

Schwarz, A.-M., Brandl, M., Kaiser, T., & Datzmann, A. (2017): Interactive mathematical maps for de-fragmentation. In: T. Dooley, G. Gueudet (Eds.): Proceedings of the Tenth Congress of the European Society for Research in Mathematics Education (CERME10, February 1-5, 2017) (pp. 2292–2293). Dublin: DCU Institute of Education and ERME. https://hal.archives-ouvertes.fr/CERME10-TWG14/hal-01941304v1

Staatsinstitut für Schulqualität und Bildungsforschung München (ISB). LehrplanPLUS, Mathematik, Fachprofile. https://www.lehrplanplus.bayern.de/fachprofil/gymnasium/mathematik.

Tall, D. (2008). The Transition to Formal Thinking in Mathematics. Mathematics Education Research Journal, 20 (2), 5–24. https://doi.org/10.1007/BF03217474

Thomas, M. O. J., De Freitas Druck, I., Huillet, D., Ju, M.-K., Nardi, E., Rasmussen, C., & Xie, J. (2015). Key mathematical concepts in the transition from secondary to university. In S. J. Cho (Ed.), The Proceedings of the 12th International Congress on Mathematical Education (pp. 265–284). New York: Springer.

Vinerean, M., Liljekvist, Y., Brandl, M., & Przybilla, J. (in press). Didactical usefulness of Interactive Mathematical Maps – Designing activities supporting student teachers’ learning. In M. Misfeldt, U. T. Jankvist, E. Geraniou, I. H. Hojsted, A. L. Tamborg, R. J. E. Coopman & B. E. Jessen (Eds.), Nordic Studies in Mathematics Education – Nordisk Matematikkdidaktikk, NOMAD – Thematic Issue Digital resources in mathematics education, 28(3-4).

Winsløw, C., & Grønbæk, N. (2014). Klein’s double discontinuity revisited: contemporary challenges for universities preparing teachers to teach calculus. Recherches en Didactique des Mathématiques, 34(1), 59–86. https://www.researchgate.net/publication/243963587

Wood, D., Bruner, J., & Ross, G. (1976). The Role of Tutoring in Problem-Solving. Journal of Child Psychology and Psychiatry, 17, 89–100. https://doi.org/10.1111/j.1469-7610.1976.tb00381.x

About the authors

name: Prof. Dr. Matthias Brandl

institution: Professur für Didaktik der Mathematik

website: https://www.fim.uni-passau.de/didaktik-der-mathematik

Matthias Brandl ist seit 2011 Inhaber der Professur für Didaktik der Mathematik an der Universität Passau. Seine Forschungsgebiete liegen in den Bereichen Vernetzungen in der Mathematik und im Mathematikunterricht, Mathematik in Schule und Hochschule, Mathematische Begabung und Kreativität, Digitale Medien im Mathematikunterricht, Narrative Didaktik und Geschichte der Mathematik.

name: Prof. Dr. Tobias Kaiser

institution: Professur für Reine Mathematik

website: https://www.fim.uni-passau.de/professur-reine-mathematik/

Tobias Kaiser ist seit 2009 Inhaber der Lehrprofessur Mathematik / Professur für Reine Mathematik an der Universität Passau. Er arbeitet in seiner Forschung auf den Gebieten der Modelltheorie (O-minimale Strukturen und ihre Verbindungen zur Analysis), Reelle Algebraische Geometrie und Reelle Analytische Geometrie sowie Reelle Algebra und Kommutative Algebra

name: Johannes Przybilla

institution: Professur für Didaktik der Mathematik

website: https://www.fim.uni-passau.de/didaktik-der-mathematik/

Johannes Przybilla promoviert an der Universität Passau in der Didaktik der Mathematik. Er hat Lehramt an Gymnasien für die Fächer Mathematik und Sport studiert. Arbeitsschwerpunkt stellt der Einsatz von digitalen Medien im Mathematikunterricht dar. Dabei liegt das Hauptaugenmerk darauf, wie digitale Medien zu einem schüleraktivierenden Mathematikunterricht beitragen können, in dem Schülerinnen und Schülern ein akkurates Bild vom Wesen der Mathematik entwickeln können. Als wissenschaftlicher Mitarbeiter in der Didaktik der Mathematik beschäftigte sich Johannes Przybilla von 2019 bis 2021 mit der Weiterentwicklung der Digitalen Mathematischen Maps / Landkarten im Bereich der Geometrie und Algebra.

name: Dr. Urs Hackstein

institution: Professur für Didaktik der Mathematik

website: https://www.fim.uni-passau.de/didaktik-der-mathematik

Nach einem Studium der Mathematik und Physik in Münster und einem Forschungsaufenthalt in Paris promovierte Urs Hackstein an der Universität Münster im Fach Mathematik. Anschließend arbeitete er als Dozent an der Universität Ulm. Danach war er in interdisziplinärer Zusammenarbeit mit Physikern, Informatikern, Medizinern und Medizintechnikern in Forschungsprojekten an der Universität in Saarbrücken und den Hochschulen in Pforzheim und Gießen tätig. Seit 2022 ist Urs Hackstein wissenschaftlicher Mitarbeiter in der Didaktik der Mathematik an der Universität Passau und beschäftigt sich hier mit der Weiterentwicklung der Digitalen Interaktiven Maps / Landkarten im Bereich der Analysis.