23 Angewandte Mathematik im Passauer Mathe-Museum: Ein Lehrkonzept zur Verzahnung von Mathematik und Didaktik

Brigitte Forster-Heinlein und Elena Mille

Abstract

Wir stellen unser innovatives Unterrichtskonzept Hands-On Mathematik von Studierenden für Schülerinnen und Schüler vor. Es besteht aus Seminaren oder Abschlussarbeiten, in welchen Studierende greifbare mathematische Exponate für Schülerinnen und Schüler entwickeln. Zusätzlich zu den üblichen Anforderungen an eine schriftliche Seminar- oder Abschlussarbeit in der Mathematik entwerfen die Studierenden instruktive Ausstellungsstücke, die mathematische Sachverhalte auf spannende Weise vermitteln. Mit dem Passauer Mathe-Museum bieten wir unseren Studierenden eine Plattform, auf der sie ihre Arbeiten dauerhaft und sichtbar präsentieren können. Die Aussicht, ihr Exponat in unserem Museum ausstellen zu können, motiviert die Studierenden, sich intensiv mit der mathematischen Theorie und ihrer didaktischen Darstellung auseinanderzusetzen.

Unser Unterrichtskonzept hat folgende Effekte. Die Studierenden arbeiten sich tief in das mathematische Thema ein, um auf Fragen der Lehrkräfte, aber auch der Schülerinnen und Schüler, der Besuchenden und der Presse gut vorbereitet zu sein. Bei der Präsentation ihrer Arbeiten trainieren die Studierenden Soft Skills wie das freie Sprechen in der Öffentlichkeit, Motivieren, Leiten und Reagieren auf Besuchende, und weitere. Bei der Gestaltung ihrer Exponate setzen insbesondere die Lehramtsstudierenden die im Didaktik-Unterricht erlernten Methoden selbstständig um. Sie üben, fachliche und fachdidaktische Aspekte zu verbinden.

Index Terms: Aktives Lernen, forschendes Lernen, vernetztes Lernen, Aktionsforschung im Klassenzimmer, MINT-Bildung, mathematische Modellierung, praxisnahe Exponate, Gamification

Angewandte Mathematik im Passauer Mathe-Museum_pdf

1. Mathematik-Ausbildung in Passau: Breite Zielgruppe mit vielfältigen Ansprüchen

In dem legendären Buch „Lyon hunting & other mathematical pursuits“ kommentiert der Mathematiker R. P. Boas Jr. in seinem Aufsatz „Can we make mathematics intelligible?“ über die Mathematik-Lehramtsausbildung (Boas, 1996, S. 230-237):

I used to advise neophyte teachers: ‘Think of what your teachers did that you particularly disliked—and don’t do it.’ This was a good advice as far as it went, but it didn’t go far enough. My tentative answer to the question in my title is, ‘Yes; but don’t be guided by introspection.’ You cannot expect to communicate effectively (whether in the classroom or in writing) unless and until you understand your audience. This is not an easy lesson to learn.

Das trifft sehr genau die Fragen, die sich zum SKILL.de-Projektbeginn für die Mathematik-Ausbildung insgesamt gestellt haben: Wie lehrt man Mathematik für eine sehr heterogene Gruppe von Studierenden? An der Universität Passau unterrichten wir Mathematik für Bachelor-/Master-Studierende und Lehramtsstudierende, aber auch für Studierende der Informatik und Ingenieure im Bereich Mobile und Eingebettete System resp. Künstliche Intelligenz. Sie alle müssen wir motivieren, sich in die Mathematik zu vertiefen und ihre mathematischen Ergebnisse allgemeinverständlich zu präsentieren. Eine besondere Herausforderung besteht darin, Studierende davon zu überzeugen, dass Beweise der Sätze lohnend sind, da sie das Fundament der Mathematik bilden. Außerdem wollen wir die Lehramtsstudierenden erkennen lassen, dass Didaktik und Mathematik tatsächlich Hand in Hand gehen. Wir wollen sie motivieren, als MINT-Botschafterinnen und MINT-Botschafter an ihren Schulen zu wirken.

Mit unserem neuartigen Unterrichtskonzept „Mathematik zum Anfassen von Studierenden für Schülerinnen und Schüler“ haben wir in unserem Passauer Mathe-Museum eine Lösung für diese Anforderungen entwickelt, die den Ehrgeiz der Studierenden aufgreift und sie antreibt. Zusätzlich zu den üblichen Anforderungen an eine schriftliche Seminar-Arbeit oder Abschlussarbeit in der Mathematik konzipieren die Studierenden ein instruktives Ausstellungsstück, das Schülerinnen und Schülern den mathematischen Sachverhalt auf attraktive Art vermittelt. Diese Exponate können ein mathematischer Apparat, Videos, Workshops, Poster oder Lehrmaterialien sein. Mit dem Passauer Mathe-Museum bieten wir den Studierenden eine Plattform, auf der sie ihre Arbeiten dauerhaft und sichtbar präsentieren können. Mit unserem Unterrichtskonzept lernen unsere Studierenden die mathematische Theorie tiefgreifend zu erfassen und trainieren, ihr mathematisches Thema einem breiten Publikum zu vermitteln. Bei den Lehramtsstudierenden legen wir einen Schwerpunkt auf Demarginalisierung und Defragmentierung. Wir haben einige Aspekte des studentischen Lernens in unserem Unterrichtskonzept durch Aktionsforschungen zu Student-Generated Questions, Certainty Based Marking und Bewertungsmatrizen zur Eigen- und Fremdbewertung evaluiert.

Es gibt etliche Veröffentlichungen zum anschaulichen Mathematikunterricht für Schüler und Schülerinnen (z. B. Guberman/Flexer/Flexer/Topping, 1999, S. 285-298; Humenberger/Hanisch/Reichel, 1991) zur Gestaltung von Ausstellungen (z. B. Letourneau/ Liu/Donnelly/Meza/Uzzo/Culp, 2019, S. 131-145; Saraniero/Kelton, 2019, S. 545-555; Phichai/Williamson/Barr, 2021) und zur Vermittlung von Mathematik mit Hilfe von Hands-on-Materialien (z. B. Luotoniemi, 2022, S. 104-120; Henderson/Taimida, 2001, S. 17-28), um nur einige zu nennen. Die Kombination dieser Bereiche, d. h. das Konzept, mathematische Kenntnisse und Fähigkeiten zu vermitteln, indem man Studierende ein lehrreiches Exponat entwerfen und dieses den Schülerinnen und Schülern präsentieren lässt, scheint unseres Wissens jedoch neu zu sein.

Im folgenden Abschnitt stellen wir das Passauer Mathe-Museum und in Abschnitt 3 das Lehrkonzept vor. In Abschnitt 4 beschreiben wir die Wirkung des Lehrkonzepts. Unseren Umgang mit Leistungsunterschieden und Vorwissen behandeln wir in Abschnitt 5, die Einhaltung mathematischer Standards in Abschnitt 6. Unsere Action Research Projekte zu Lehr-Lernforschung und die Auswirkungen der Corona-Pandemie auf unsere Lehre fassen wir in Abschnitt 7 zusammen. Wir schließen mit einem Ausblick in Abschnitt 8.

2. Das Passauer Mathe-Museum

An der Universität Passau betreiben wir ein Mathematik-Museum, das Schülerinnen und Schülern über Ausstellungstücke zum Anfassen einen neuen Blick auf die Mathematik ermöglichen soll. Das Museum bietet eine große Zahl von Puzzles und Rätseln, wie zum Beispiel

  • zu optimalen Packungen, ein Problem aus der Logistik (Abbildung 1)
  • zu projektiven Ebenen und deren Zusammenhang zu den bekannten Kartenspielen SET und Dobble (Abbildung 2),
  • zum Museumswächter-Problem aus der algorithmischen Geometrie (Abbildung 3)

und anderen. Das Museum beherbergt weiter große Geräte, die mathematisch-physikalische Effekte erlebbar machen. Hier sind zum Beispiel zu nennen:

  • die Abtasttrommel, die Schwingungen von Bass-Saiten sichtbar macht, und die Schwierigkeiten der Abtastung/Digitalisierung von Ton-Signalen visualisiert,
  • der Tornado, der es erlaubt, die zwei Phasen des Differentialgleichungsmodells dieses Windphänomens zu manipulieren und zu untersuchen (Abbildung 4),
  • die Chladni-Figuren, die Töne anhand von Klangfiguren sichtbar machen (Abbildung 5).

Ein online Angebot an Web-Applets und Filmen rundet das Angebot ab. Beispielsweise bietet das Museum Webseiten[1] zu den Themen

  • Bézier-Kurven, die für Design und Konstruktion eine große Rolle spielen (Abbildung 6),
  • Moiré-Effekt, den man zum Beispiel beobachtet, wenn man zwei Lagen Tüll-Stoff übereinanderlegt und verschiebt,
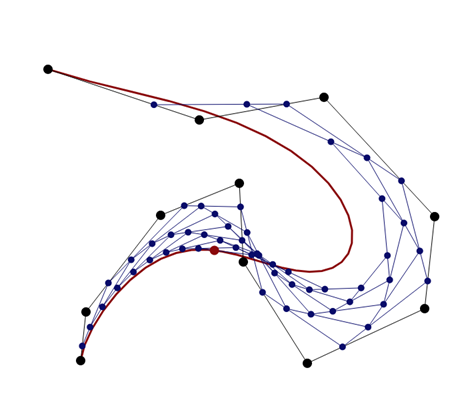
  • Verfolgungskurven (Abbildung 7)
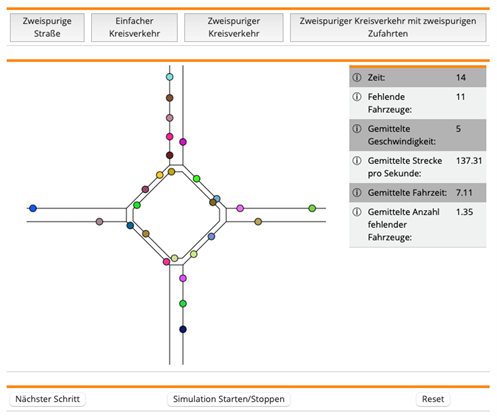
  • Verkehrssimulation (Abbildung 8),

und weitere[2].

Die Filmreihe „Passauer MINT-Bonbons“ bietet eine zugängliche Aufbereitung moderner Themen aus der Mathematik[3]. Über die Ausstellungsstücke, die Applets und die Filme lernen die Schülerinnen und Schüler neue Aspekte und aktuelle Anwendungen der Mathematik kennen.

Das Passauer Mathe-Museum wurde 2012 von der Erstautorin gemeinsam mit Kollegen an der Fakultät gegründet. Es hat sich über die Jahre zu einem Museum von Studierenden für Schülerinnen und Schüler entwickelt. Alle oben genannten Exponate und zahlreiche weitere wurden von Studierenden im Rahmen von Seminaren und Abschlussarbeiten entwickelt.

3. Das Lehrkonzept

Um das Passauer Mathe-Museum zu erweitern und auszubauen, bieten die Autorinnen Seminare zum Thema „Angewandte Mathematik im Passauer Mathe-Museum“ an. Die Studierenden wählen aus einer Sammlung geeigneter Fragestellungen ein Thema nach ihren Neigungen. Sie recherchieren den mathematischen Sachverhalt und stellen diesen in einer schriftlichen Ausarbeitung zusammen. Anschließend präsentieren sie ihre Ergebnisse in einem Seminar-Vortrag. Zusätzlich zu diesen üblichen Seminar-Anforderungen reduzieren die Studierenden die Mathematik und entwickeln ein instruktives Ausstellungsstück für unsere Besucherinnen und Besucher im Passauer Mathe-Museum. Das Exponat kann ein Ausstellungsstück zum Anfassen, ein Kurzfilm, ein Poster, ein Web-Applet, Unterrichtsmaterialen oder ähnliches sein. Im Rahmen von Tagen der offenen Tür oder Schulbesuchen können die Studierenden ihre Werke Schülerinnen und Schülern und der Öffentlichkeit präsentieren.

Die Ziele unseres Lehrkonzepts im Seminar sind dabei folgende (Forster-Heinlein/Epperlein/Mille, 2022):

(1) Vertiefte mathematische Kompetenz: Das Ziel, das Exponat der Öffentlichkeit zu präsentieren, veranlasst die Studierenden, sich umfassend über die mathematischen Sachverhalte zu informieren, um auf Fragen der Fakultät, der Schülergruppen und auch der Presse vorbereitet zu sein. Unser breites Publikum erfordert, dass Studierende die Mathematik ihres Exponats erstens tief verstehen und erklären können und zweitens in den Anwendungskontext stellen können. Die Studierenden erarbeiten sich umfangreiche mathematische Kenntnisse, um auf alle Fragen adäquat antworten zu können. Zum Vergleich: Bei Standardseminaren bleiben die Studierenden in der Regel bei dem vorgegebenen Lehrbuch oder Artikel, während sie in unserem Seminar durchschnittlich sieben wissenschaftliche Bücher oder Aufsätze recherchieren, um ihre Präsentation zu untermauern.

(2) Erwerb von Schlüsselkompetenzen: Bei der Präsentation ihrer Arbeit im Rahmen des Seminars und bei der Präsentation des Exponats vor Schulklassen trainieren die Studierenden Soft Skills wie Auftritt, Rhetorik, Präsentationstechniken, Motivation, Führung und das Eingehen auf die BesucherInnengruppen. Um dieses Ziel zu erreichen, haben wir ein zweistufiges Verfahren implementiert: Jede:r Studierende hält zunächst eine Midterm-Präsentation, in der er oder sie über die Zwischenergebnisse berichtet und Feedback von den Kommiliton:innen und von den Dozierenden erhält. Zweitens verteidigen die Studierenden ihre Seminar- oder Abschlussarbeiten in ihren Abschlusspräsentationen (vor Publikum in der Regel aus Fakultätsmitgliedern). Wir als Dozierende und auch die Mitstudierenden beobachten Verbesserungen von der Zwischenpräsentation zur Abschlusspräsentation. Diese Verbesserungen umfassen Soft-Skill-Aspekte wie Rhetorik, Organisation der Präsentation und selbstbewusstes Auftreten. Wir veranstalten regelmäßig Tage der offenen Tür, zu denen wir auch die Presse einladen. Hier lernen die Studierenden, ihre mathematischen Arbeiten und ihr Exponat der Öffentlichkeit zu präsentieren. Für die meisten Studierenden ist dies der erste Kontakt mit Fragen von Pressevertretern – eine wichtige Erfahrung.

(3) Demarginalisierung in der Lehrkräftebildung: Das gemeinsame Memorandum zur Gymnasiallehrerbildung der Deutschen Mathematiker Vereinigung DMV und der Gesellschaft für Didaktik der Mathematik (GDM) notiert (Stroth/ Törner/Scharlau/Blum/Reiss, 2021):

Es ist ‚für die zukünftigen Lehrerinnen und Lehrer von prägender Bedeutung, bereits im Studium zu erfahren, dass es in der Mathematik unzählige offene Fragen gibt, durch deren Bearbeitung sich die Mathematik auch aktuell ausformt und dynamisch weiterentwickelt. Lehramtsstudenten müssen über die Aneignung von Faktenwissen hinaus befähigt werden, auch ein exploratives und heuristisches Vorgehen als grundlegende Arbeitsformen der Mathematik zu begreifen.‘

Bei der Konzeption und Entwicklung des Exponats erarbeiten die Studierenden Lösungen, wie sie Schülerinnen und Schülern wie auch Laien die mathematischen Fakten durch Experimente näherbringen können. Mit ihrem Exponat werden sie zu Botschafterinnen und Botschaftern der Mathematik: Da ihr Exponat mit ihrem Namen im Passauer Mathe-Museum verbleibt, bekommen die Studierenden eine langanhaltende Sichtbarkeit und Anerkennung. (4) Defragmentierung durch Anwendung didaktischer Methoden: Die Studierenden setzen die in den Didaktik-Vorlesungen erlernten Methoden selbstständig mit ihrem Exponat um. Die Lehramtsstudierenden lernen, fachspezifische und fachdidaktische Aspekte miteinander zu verzahnen. Für die Lehramtsstudierenden ist das Seminar in der Regel die erste Gelegenheit, ein mathematisches Problem gleichzeitig aus fachwissenschaftlicher und didaktischer Sicht zu beleuchten. (An der Universität Passau sind Mathematik und Lehramtsbildung gar an verschiedenen Fakultäten angesiedelt. Der interfakultäre wissenschaftliche Austausch zur Lehrkräftebildung beschränkt sich auf wenige Professuren). Die Lehramtsstudierenden gehen in ihrer Arbeit auf beide Aspekte – Mathematik und Fachdidaktik ein, da beides Pflichtbestandteile der schriftlichen Arbeit sind. Für die Präsentation ihres Exponats entwickeln sie eine mathematikdidaktische Erklärung für die Museumsbesucher.

4. Wirkung des Lehrkonzepts

Die oben genannten Punkte „Vertiefte mathematische Kompetenz“ und „Erwerb von Schlüsselkompetenzen“ sind für alle unsere Studiengänge wichtig: Die Studierenden werden durch die Aussicht, ihre Arbeiten öffentlich zu präsentieren, besonders motiviert, sich tief und breit mit dem mathematischen Thema auseinanderzusetzen. Sie absolvieren ihre Präsentationen vor Fachpublikum in der Fakultät und werden parallel dazu auf Fragen zu Anwendungen, Sinn und Zweck des Themas vorbereitet, wie sie beispielsweise von Museumsbesucherinnen und -besuchern gestellt werden.

Für Lehramtsstudierende bieten wir ein Übungsfeld, um die in den Didaktik-Vorlesungen erlernten Techniken selbstständig auf ein eigenes Thema anzuwenden. Die Studierenden erarbeiten eine Lösung, wie sie die komplexe mathematische Fragestellung für unsere Museumsbesuchende angemessen und fachlich korrekt reduzieren können.

Auch für Studierende anderer Studiengänge ist es wichtig, mathematische Sachverhalte an Nicht-Mathematiker:innen vermitteln zu können. Für Informatikstudierende, die beispielsweise Applets für die Website des Museums entwickeln, bieten wir über das Online-Museum ein Trainingsfeld, um ihre Kompetenzen in den Bereichen Human Interfaces („intuitiv, lernbar, konsistent“) und Gamification zu schärfen, damit sie ihr mathematisches Thema bestmöglich transportieren können (Knapp, 2012; Krug, 2006; Heath & Heath, 2007).

Weitere Ziele unseres Konzepts sind die Schulung der Präsentationsfähigkeiten von Studierenden aller Studiengänge und die Stärkung ihres Selbstbewusstseins. Unser Konzept motiviert die Studierenden intrinsisch. Eine wissenschaftliche Arbeit zu verfassen und ein Exponat zu entwickeln, das man später Freund:innen, Eltern, Kolleg:innen oder den eigenen Schulkindern zeigen kann, ist ein großer Anreiz.

Über das Passauer Mathe-Museum machen wir die Beiträge unserer Studierenden sichtbar. Zulassungsarbeiten (d.h. Hausarbeiten für die Zulassung zur allgemeinen bayerischen Staatsprüfung für das Lehramt) werden in den bayerischen Bibliotheken in der Regel nicht zugänglich gemacht – im Gegensatz zu Bachelor- und Masterarbeiten; Zulassungsarbeiten sind weitgehend unsichtbar. Die Transparenz, die das Museum als Plattform bietet, führt bei unserem Lehrkonzept dazu, dass alle Studierenden auf dem gleichen Informationsstand sind und von ihren Vorgänger:innen lernen. Best Practices werden so ohne zusätzlichen Aufwand an die nächste Studierenden-Generation weitergegeben.

5. Umgang mit Vorqualifikationen und Leistungsunterschieden

Wir bieten unseren Studierenden ein breites Spektrum an mathematischen Themen im Rahmen der Forschungsschwerpunkte unseres Fachbereichs, d.h. von der theoretischen Mathematik bis hin zu Anwendungen in der Informatik. Dies gibt uns den nötigen Raum, auf die unterschiedlichen Studienrichtungen und Vorqualifikationen unserer Studierenden einzugehen.

Wir lassen unseren Studierenden die Freiheit der konkreten Gestaltung des Exponats. Wir ermutigen sie, ihre kreativen Neigungen und handwerklichen Fähigkeiten in die Arbeit einfließen zu lassen. Unterschiedliche Lernstile führen zu unterschiedlichen Exponaten, von Hands-On-Maschinen aus Holz bis hin zu JavaScript-Applets. In King&Lord, 2016 wird diese Methode des vernetzten Lernens vorgeschlagen, um persönliche Interessen mit Akademiker:innen und anderen Gleichgesinnten zu verbinden. Definiert als Lernen, das sozial eingebettet, interessengesteuert und auf bildungsbezogene, wirtschaftliche oder politische Möglichkeiten ausgerichtet ist (Ito et al., 2013), wird festgestellt, dass Studierende am besten lernen, wenn sie sich für den Lernstoff interessieren und diese Interessen in einer Gemeinschaft von Gleichgesinnten erkunden können.

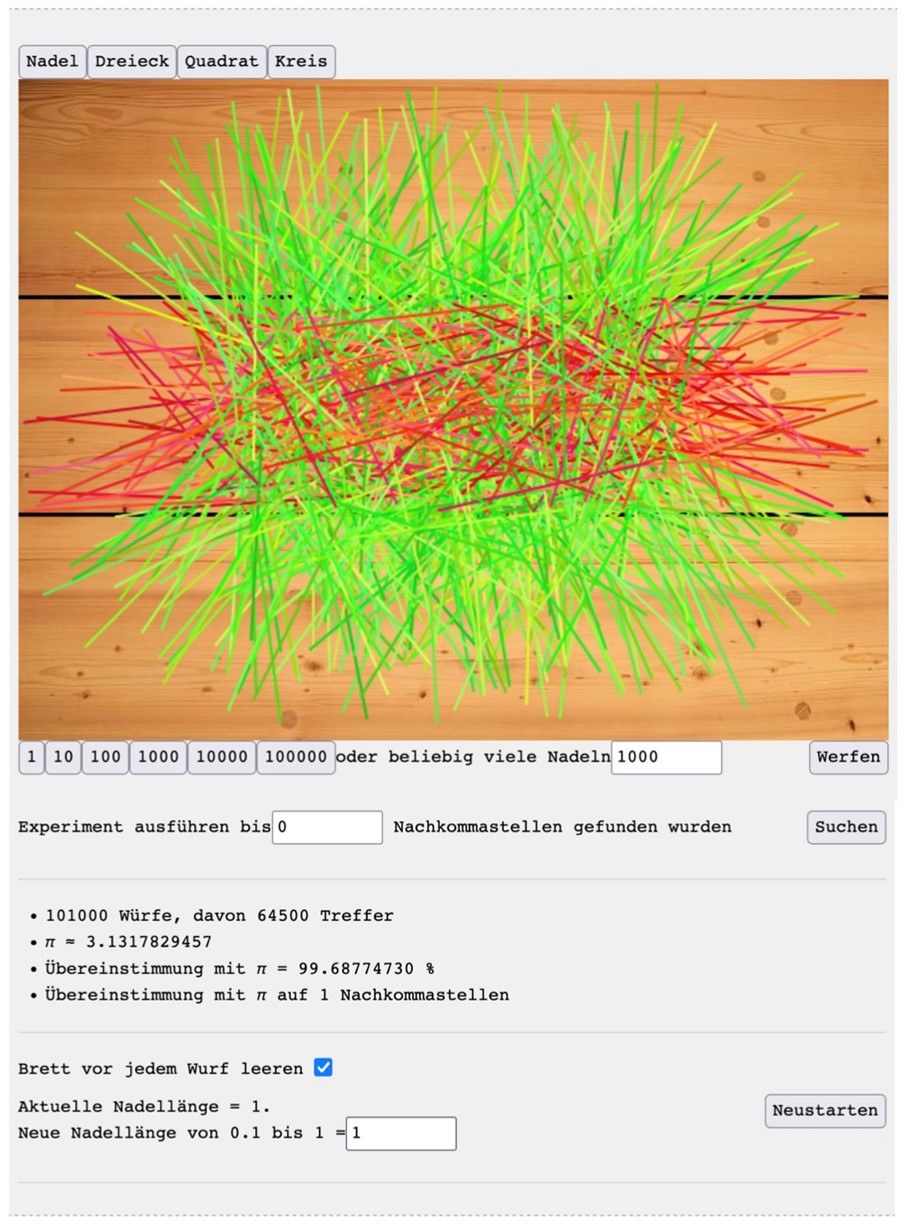
Im Studiengang Internet Computing unserer Fakultät ist die Entwicklung von Applets sehr beliebt (zum Beispiel die Simulation des Buffon-Experiments, siehe Abbildung 9). Informatik- und Mathematikstudierende bevorzugen oft theoretische Arbeiten, die sie in Postern oder praktischen Exponaten aufbereiten (z. B. die Lissajous-Maschine, siehe Abbildungen 10 und 11, oder Minimalflächen, siehe Abbildung 12). Lehramtsstudierende wenden ihre pädagogisch-didaktische Ausbildung an und entwickeln Experimente für unsere jungen Museumsbesuchenden (z. B. Experimentierkasten zur Knotentheorie, siehe Abbildung 13).

Wir folgen einem guided inquiry Ansatz, eine Methode, die Studierenden, die aufgrund mangelnder Erfahrung, mangelnden Wissens oder weil sie noch nicht genügend in abstraktem Denken trainiert sind, nicht in der Lage sind, Untersuchungsprobleme ohne Anleitung zu bewältigen, mehr Orientierung bietet. Ziel ist es, dass die Lehrenden durch ihre Fragen die Studierenden anleiten und somit die Frustration senken und gleichzeitig ein hohes Maß an intellektueller Herausforderung aufrechterhalten (Gormally/Brickmann/Hallar/Armstrong, 2009).

Die folgenden Schlüsselkompetenzen werden durch unser Unterrichtskonzept gestärkt:

  • Über das Exponat: mathematische Fähigkeiten und technische Grundkompetenzen, Eigeninitiative und Verantwortung, Kreativität, Zeitmanagement.
  • Über die Präsentation: Öffentliches Auftreten und Performance, Rhetorik, Kritikfähigkeit, Kommunikationsfähigkeit, Medienkompetenz.

6. Einhaltung mathematischer Standards

Mathematische Gesetzmäßigkeiten als Theorem zu formulieren und zu beweisen ist die Grundlage mathematischer Arbeit. In unseren Seminaren und für die Abschlussarbeiten verlangen wir, dass die Studierenden mindestens ein mathematisches Theorem, das zu ihrem Thema beiträgt, vorstellen und beweisen müssen. Natürlich ist es oft schwierig, Nicht-Mathematikstudierende davon zu überzeugen, sich in einen Beweis zu vertiefen. Es braucht eine große Anzahl von Beispielen, um allen die Bedeutung von Beweisen klarzumachen (Bauer/Müller-Hill/Neuhaus-Eckhardt/Rach, 2021). In unseren Seminaranweisungen machen wir unmissverständlich klar, dass das Formulieren und Beweisen eines mathematischen Satzes zentrale Anforderungen sind. Inzwischen haben wir beobachtet, dass die Studierenden aller Studiengänge selbst darauf bestehen, dass ihre Kommilitoninnen und Kommilitonen Beweise für ihre Behauptungen vorlegen. Wir haben in unseren Seminaren eine mathematische Kultur etabliert, die von den Studierenden selbst gepflegt und verteidigt wird.

Ein Beispiel für die Bedeutung, die unsere Studierenden Beweisen beimessen, sind die beiden Filme, die ein Student über das Theorema Egregium und Kartenprojektionen produziert hat. Sein erster Film erklärt, warum alle flachen Landkarten der Erde verzerrt sind. In seinem zweiten, zusätzlich und freiwillig produzierten Film präsentiert er die Beweise für das geneigte Publikum[4].

7. Lehr-Lern-Forschung und Lehre in der Pandemie

Für jedes Semester wählen wir einen Ansatz der Aktionsforschung zur Bewertung der Lehrleistung und der Lernerfahrung. Bisher haben wir zu

  • Student-Induced Questions (Caspari/Forster-Heinlein/Mägdefrau/Bachl, 2021)[5] und
  • Certainty-Based marking (Caspari-Sadeghi/Mille/Epperlein/Forster-Heinlein, 2022, S. 145-156) und
  • Evaluationsmatrizen / Rubrics (Caspari-Sadeghi/Mille/Epperlein/Forster-Heinlein, 2023 und Forster-Heinlein/Mägdefrau, 2023)

beigetragen. Hierfür arbeiten wir mit unseren Partner:innen aus der Lehr-Lern-Forschung zusammen. Deren Fachwissen hilft unseren Lehramtsstudierenden, neue und wirksame Techniken zur Bewertung von Wissen und Fertigkeiten in ihrem Unterricht kennen zu lernen. Die Methoden sind für Studierende aller Fachrichtungen gleichermaßen relevant, da Selbst- und Fremdeinschätzung in allen beruflichen Kontexten eine Rolle spielen.

Während der Covid-19 Pandemie haben wir unser Seminar auf ein virtuelles Format umgestellt. Die Studierenden präsentierten sich gegenseitig den Stand ihrer Arbeit in Online-Seminaren und untersuchten die Wirkung ihrer Exponate. Unsere Studierenden waren so motiviert, dass die meisten von ihnen neben dem praktischen ein zusätzliches digitales Exponat entwickelten. Für die entstandenen Filme haben wir nun eine Kurzfilmreihe „Passauer MINT-Bonbons“ zusammengestellt, in der ausschließlich Studierende und Nachwuchswissenschaftlerinnen und -wissenschaftler ihre Arbeiten vorstellen[6]. Diese zusätzlichen Beiträge belegen die motivierende Wirkung unseres Unterrichtskonzeptes.

Aufgrund der Pandemie konnten viele Monate keine Besuchenden ins Museum kommen. Im Rahmen unseres Forschungsnetzwerks „Aufbau eines Netzwerks von MINT-Learning Centern“, das von der Europäischen Union und Partnern aus der Wirtschaft gefördert wird, tragen wir zu MINT-Onlinekursen für Schulklassen bei. Sie heißen „online MINTwochs“, wurden von unseren Kolleginnen und Kollegen der ScienceCity Itzling, Österreich, ins Leben gerufen und finden mittlerweile monatlich statt[7]. Mit dieser internationalen Zusammenarbeit von MINT-Zentren aus Linz, Salzburg, Itzling (alle Österreich) und Passau (Deutschland) erreichen wir ein viel größeres Publikum und können ein breites Spektrum an MINT-Themen für Schulklassen anbieten.

Inzwischen beteiligen sich unsere Studierenden regelmäßig an diesen Online-Workshops mit ihren mathematischen Projekten zu Knotentheorie, Kartenprojektionen (Abbildung 14) und mathematischen Kartentricks (Abbildung 15). Trotz der Corona-Pandemie haben wir damit für sie ein Übungsfeld geschaffen, in dem sie die Methoden der virtuellen Wissensvermittlung üben und evaluieren können.

Es gibt weitere Mathematikmuseen zum Anfassen in Deutschland, zum Beispiel das Mathematikum in Gießen[8], das ix-quadrat in München[9], das Erlebnisland Mathematik in Dresden[10]. Keines dieser Museen ist auf die Ausbildung von Studierenden ausgerichtet, vielmehr sind Schulklassen, Lehrkräfte und die interessierte Öffentlichkeit die Zielgruppe. Dies zeigt sich bei öffentlichen Auftritten, bei Besuchen und in persönlichen Gesprächen mit den Verantwortlichen. Studierende werden bei Museumsführungen als Explainers eingebunden, treten aber nicht als Exponat-Entwickler auf. Auf den Websites dieser Museen findet sich kein Hinweis auf ein pädagogisches Konzept. Diese Museen haben eine andere Zielsetzung als wir mit dem Passauer Mathe-Museum. In unserem Lehrkonzept stehen die Studierenden im Mittelpunkt. Das Passauer Mathe-Museum bietet den Studierenden eine Plattform für ihre Sichtbarkeit und zur Interaktion mit Schulklassen. Unser Lehrkonzept für Mathematik zum Anfassen von Studierenden für Schülerinnen und Schülern, bei dem die Studierenden den gesamten Weg von der mathematischen Theorie über die Reduktion auf das Exponat bis hin zur persönlichen Präsentation vor unseren Besuchern trainieren können, ist daher unseres Wissens ein Novum. Auch die Namen der Schöpfer:innen auf den Exponaten im Museum sind eine Besonderheit, die die Leistungen unserer Studierenden langfristig sichtbar machen und sie an unsere Universität binden. Die Exponate der Studierenden werden im Museum aktiv genutzt. Kolleginnen und Kollegen unserer Fakultät veranstalten Lehrkräftefortbildungen im Passauer Mathe-Museum, organisieren Besuche von Schulklassen, bei Mathe-Wettbewerben oder auch einfach nur, um Gästen die Arbeiten unserer Studierenden zu zeigen. Die Studierenden erfahren so eine zusätzliche Wertschätzung als sichtbarer Teil unserer Fakultät, für die es sich lohnt, besondere Anstrengungen zu unternehmen.

8. Schlussfolgerung und Ausblick

Mit unserem Lehrkonzept „Mathematik zum Anfassen von Studierenden für Schülerinnen und Schüler“ erreichen wir mehrere Ziele. Unsere Studierenden vertiefen sich in ein mathematisches Thema, um a) ihre Abschlussarbeit zu schreiben, b) ein anschauliches Exponat zu gestalten und c) dieses vor einem breiten Publikum zu präsentieren. Auf diesem Entwicklungspfad lernen sie nicht nur die mathematische Theorie kennen, sondern setzen sich auch mit der didaktischen Reduktion auseinander. Außerdem entwickeln sie Strategien, um ihr mathematisches Thema sowohl Fachpublikum (also Dozent:innen und Studierenden) als auch Schülerinnen und Schülern zu erklären. Als Nebeneffekt haben wir ein gut ausgestattetes Mathe-Museum, das Schulklassen offensteht. Unsere Studierenden bieten Workshops (online und in Präsenz) zu ihren Exponaten an. Auf diese Weise sammeln die Lehramtsstudierenden Erfahrungen mit Schulkindern. Unser nächster Schritt ist die Evaluierung des Lernens im Museum. Das Lernen und die Bewertung des Lernens in Ausstellungen (siehe z. B. Thuneberg/Salmi, 2017; Gibbs/Sani/Thompson, 2007) ist ein Forschungsgebiet, das immer mehr in den Fokus rückt[11]. Wir wollen untersuchen, welche Strategien der Visualisierung und Interaktion am besten geeignet sind, um nachhaltiges Lernen zu bewirken – sowohl bei Studierenden als auch bei Schülerinnen und Schülern. Auch hier werden wir unsere Lehramtsstudierenden in die Forschung mit einbeziehen, da die Ergebnisse für ihren eigenen Unterricht wertvoll sein können.

Danksagung: Die Finanzierung erfolgte durch das Bundesministerium für Bildung und Forschung über das Projekt SKILL.de und durch die Europäische Union über das Interreg-Projekt AB 307. Brigitte Forster-Heinlein wurde für ihr Unterrichtskonzept im Passauer Mathe-Museum mit dem Ars Legendi-Fakultätenpreis in Mathematik 2021 durch den Stifterverband ausgezeichnet.

Abbildungen

 

Abbildung 1. Optimale Kreispackungen. Ein Hands-On Puzzle von Fabian Blochberger zu einem Thema mit praktischer Anwendung und noch vielen offenen mathematischen Forschungsfragen
Abbildung 2. Eine Dobble-Variante von Jonathan Adler illustriert das Konzept der projektiven Ebenen in der Geometrie
Abbildung 3. Das Museumswächterproblem aus der Algorithmischen Geometrie aus Holz und mit LEDs von Bernhard Andraschko
Abbildung 4. Tornado zur Illustration eines Zwei-Phasen-Differentialgleichungssystems von Martin Herrndobler. Ausschnitt aus einer filmischen Aufbereitung der Zweitautorin
Abbildungen 5. Schwingungsmuster in der Ebene und die verschiedenen physikalischen Modi illustriert die mit Sand bestreute Chladni-Platte, wenn man sie mit dem Geigenbogen streicht. Ausstellungsstück von Carina Nunweiler.
Abbildung 6. Interaktives Applet zu Bezier-Kurven, die beim Computer Aided Design eine große Rolle spielen, von Andreas Finsterwalder
Abbildung 7. Was passiert, wenn ein Käfer einen Käfer verfolgt, der einen Käfer verfolgt, der einen Käfer verfolgt, der … Die entstehenden Verfolgungskurven visualisiert das Applet von Siegfried Steckenbiller
Abbildung 8. Staus im doppelspurigen Kreisverkehr lassen sich mit dem Applet von Maximilian Ettelt erforschen
Abbildung 9. Website des JavaScript-Applets zur Veranschaulichung der statistischen Schätzung der Zahl Pi anhand des Buffonschen Experiments. Applet von Stefan Becher.
Abbildung 10. Die Lissajous-Maschine, gebaut mit schweren 15 kg Gewichten für eine lange und stabile Bewegung. Zwei in orthogonalen Ebenen schwingende Pendel treiben zwei übereinander liegende Rollbretter an, auf welchen obenauf ein Blatt Papier befestigt ist. Ein feststehender Stift macht die Bewegung der Rollbretter sichtbar. Exponat von Linda Rank (Mitte).
Abbildung 11. Ein Beispiel einer Lissajous-Figur, das von der Maschine in Abbildung 10 gezeichnet wurde.
Abbildung 12. Experiment zu Minimalflächen von Kerstin Bichler. Mit Seifenlauge lassen sich Minimalflächen über verschiedene Randobjekte, hier ein Würfel, untersuchen.
Abbildung 13. Experimentierkasten zur Knotentheorie von Lena Bachl. Die Schülerinnen und Schüler erfahren, dass mathematisch gleiche Knoten unterschiedlich aussehen können. Sie lernen grundlegende Ideen zur formalen Beschreibung von Knoten kennen und entdecken Beispiele für Äquivalenzklassen von Knoten.
Abbildung 14. Online-Workshop und Film über Kartenprojektionen und das Theorema Egregium von Simon Biberger. Er erklärt die mathematischen Schwierigkeiten, kugelförmige Objekte auf die Ebene abzubilden anhand von geschälten Orangen und – wie hier zu sehen – aufgeschnittenen Fußbällen. Die Fußball-Karte regt zu Diskussionen an, unter welchen Bedingungen die Lösung eines Problems sinnvoll ist oder nicht.
Abbildung 15. Online-Workshop zu mathemagischen Kartentricks auf der Basis von Permutationsgruppen von Jonas Kosak. Schon mit einfachen Mitteln – einem Kartenspiel, Papier und Stift – können Studierende den Schülerinnen und Schülern anspruchsvollen mathematischen Inhalt transportieren.

Literatur

Bauer, T., Müller-Hill, E., Neuhaus-Eckhardt, S. und Rach, S. (2021). „Beweisverständnis im Mathematikstudium unterstützen: Vergleich unterschiedlicher Varianten der Strategie “Illustrieren am Beispiel”,“ Journal für Mathematik-Didaktik.

Beutelspacher, A. „mathematikum: Mathematik zum Anfassen,“ [Online]. Available: https://www.mathematikum.de/.

Biberger, S. „Verzerrte Welt! Warum alle Landkarten der Erde falsch sind,“ [Online]. Available: https://vimeo.com/521787420/07f00584ea.

Biberger, S. „Verzerrte Welt! Warum alle Landkarten der Erde falsch sind – Teil 2 Beweis,“ [Online]. Available: https://vimeo.com/521782985/914c555724.

Boas, R.P (1996). „Can we make mathematics intelligible?“. In: Lion Hunting and Other Mathematical Pursuits: A Collection of Mathematics, Verse, and Stories by the Late Ralph P. Boas, Jr, S. 230-237.

Caspari, S., Forster-Heinlein, B., Mägdefrau J. und Bachl, L. (2021). „Sustainable e-assessment in mathematics instruction,“ In. Exploring new ways to connect. Proceedings of the Eleventh International Mathematics Education & Society Conference, Klagenfurt, Österreich.

Caspari, S., Forster-Heinlein, B., Mägdefrau J. und Bachl, L. (2021).„Sustainable e-assessment in mathematics instruction,“ in Exploring new ways to connect. Proceedings of the Eleventh International Mathematics Education & Society Conference, Klagenfurt, Österreich.

Caspari, S., Forster-Heinlein, B., Mägdefrau, J. und Bachl, L. (2021).„Student-generated questions: Developing mathematical competence through online-assessment,“ International Journal for the Scholarship of Teaching and Learning, Bd. 15, p. Article 8.

Caspari-Sadeghi, S., Mille, E., Epperlein, H. und Forster-Heinlein, B. (2022). „Stimulating reflection through self-assessment: Certainty-based marking (CBM) in online mathematics learning,“ Mathematics Teaching Research Journal, Bd. 14, Nr. 2, S. 145-156.

Caspari-Sadeghi, S., Mille, E., Epperlein; H. und Forster-Heinlein, B. (2023). „Democratizing Assessment for Sustainable Learning in Mathematics Instruction: Giving Students Agency in Classroom Research“, In 2023 IEEE Global Engineering Education Conference Educon, Kuwait.

Forster-Heinlein, B., Epperlein H., Mille, E. (2022). „The Passau Math Museum: Hands-On Mathematics by Students for Schoolkids“, In: 2022 IEEE German Education Conference GeCon, Berlin.

Forster-Heinlein, B., Mägdefrau, J. (2023). „Action Research in der Hochschullehre: Drei Beispiele aus dem Fach Mathematik,“ Empirische Pädagogik, Eingereicht.

Gibbs, K., Sani, M und Thompson, J. (2007). Lifelong learning in museums: A European Handbook., EDISAI.

Gormally, C., Brickmann, P., Hallar, B., Armstrong, N. (2009). „Effects of inquiry-based learning on students’ science literacy skills and confidence“. International Journal for the Scholarship of Teaching & Learning, Bd. 3, Nr. 2, p. Article 16.

Guberman, S. R., Flexer, R. J., Flexer, A. S., Topping, C. L. (1999). „Project Math-Muse: Interactive mathematics exhibits for young children“. 42. Curator: The Museum Journal, S. 285-298.

Heath, C., Heath, D. (2007). Made to Stick: Why Some Ideas Survive and Others Die, Random House.

Henderson, D. W., Taimida, D. (2001). „Crocheting the hyperbolic plane“. The Mathematical Intelligencer, Bd. 23, Nr. 2, S. 17-28.

Humenberger, J., Hanisch, G., Reichel, H. C. (1991). Fachbereichsarbeiten und Projekte im Mathematikunterricht mit Anregungen für das Wahlpflichtfach, Wien: Hölder-Pichler-Tempsky.

Ito, M., Gutierrez, K., Livingstone, S, Penuel, B., Rhodes, J., Salen, K., Schor, J., Sefton-Green, J., Watkins, S. C. (2013). Connected learning: An agenda for research and design, Irvine, CA: Digital Media and Learning Research Hub.

King, B., Lord, B., (2016). The Manual of Museum Learning, 2. Auflage, Rowman & Littlefield.

Knapp, K. M. (2012). The gamification of learning and instruction: Game-based methods and strategies for training and education, Pfeiffer.

Krug, S. (2006). Don’t make me think! A common sense approach to web usability., 2. Auflage, New Riders.

Letourneau, S. M., Liu, C. J., Donnelly, K., Meza, D., Uzzo, S., Culp, K. M. (2019). „Museum Makers: Family explorations of data science through making and exhibit design“, Curator: The Museum Journal, Bd. 63, Nr. 1, S. 131-145.

Luotoniemi, T. (2022). „Stick models of projective configurations,“ Journal of Mathematics and the Arts, Bd. 16, Nr. 1-2, S. 104-120.

MINT: Labs Science City Itzling, „(Online) MINTwoch: eine virtuelle Reise in die Salzburger Forschungswelt,“ [Online]. Available: https://www.mintlabs.at/mintwoch/.

Phichai, P., Williamson, J., Barr, M. (2021). „Alternative design for an interactive exhibit learning in museums: How does user experience differ across different technologies — VR, tangible, and gesture“. In: 7th International Conference of the Immersive Learning Research Network (iLRN), IEEE.

RICHES Project, „RICHES Think Paper 06. Museum education with digital technologies: participation and lifelong learning,“ 2016. [Online]. Available: https://resources.riches-project.eu/riches-think-paper-06-museum- education-with-digital-technologies-participation-and-lifelong-learning/.

Richter-Gebert, J. „ix-quadrat: Eine Ausstellung des Zentrums Mathematik an der TU München,“ [Online]. Available: https://www-m10.ma.tum.de/ix- quadrat/index.html/.

Saraniero, P., Kelton, M. L. (2019). „Discover and Explore”: Creating impactful STEAM learning experiences for museum professionalsCreating impactful STEAM learning experiences for museum professionals“, Curator: The Museum Journal, Bd. 62, Nr. 4, S. 545-555.

Stroth, G., Törner, G., Scharlau, R., Blum, W., Reiss, K., „DMV-GDM-Denkschrift zur gymnasialen Lehrerbildung,“ Februar 2021. [Online]. Available: https://www.mathematik.de/presse/652-dmv-gdm-denkschrift-zur- gymnasialen-lehrerbildung. [Zugriff am 11 April 2023].

Technische Sammlungen Dresden, „Erlebnisland Mathematik Dresden,“ [Online]. Available: http://www.erlebnisland-mathematik.de/.

Thuneberg, K. F. H., Salmi, H. (2017). „Hands-on math and art exhibition promoting science attitudes and educational plans“, Education Research International, Bd. 2017, p. Article ID 9132791.

Universität Passau, „Passauer Mathe-Museum,“ 2023. [Online]. Available: www.mathe-museum.uni-passau.de. [Zugriff am 10 April 2023].

Universität Passau, „Digitale Exponate zum Ausprobieren,“ Passauer Mathe-Museum, 2023. [Online]. Available: https://www.mathe-museum.uni-passau.de/digitale-exponate-zum-ausprobieren. [Zugriff am 10 April 2023].

Universität Passau, „Videos: Passauer MINT-Bonbons,“ [Online]. Available: https://www.mathe-museum.uni-passau.de/videos-passauer-mint-bonbons/.

Universität Passau, „Videos: Passauer MINT-Bonbons,“ Passauer Mathe-Museum, 2023. [Online]. Available: https://www.mathe-museum.uni-passau.de/videos-passauer-mint-bonbons. [Zugriff am 10 April 2023].

Medien-Attributierungen

  1. Universität Passau, „Passauer Mathe-Museum,“ www.mathe-museum.uni-passau.de ↵
  2. Universität Passau, „Digitale Exponate zum Ausprobieren,“ Passauer Mathe-Museum, https://www.mathe-museum.uni-passau.de/digitale-exponate-zum-ausprobieren ↵
  3. Universität Passau, „Videos: Passauer MINT-Bonbons,“ Passauer Mathe-Museum, https://www.mathe-museum.uni-passau.de/videos-passauer-mint-bonbons ↵
  4. S. Biberger, „Verzerrte Welt! Warum alle Landkarten der Erde falsch sind“, https://vimeo.com/521787420/07f00584ea;S. Biberger, „Verzerrte Welt! Warum alle Landkarten der Erde falsch sind - Teil 2 Beweis“, https://vimeo.com/521782985/914c555724. ↵
  5. Caspari-Sadeghi,S., Forster-Heinlein, B., Mägdefrau, J., & Bachl, L. (2021). Student-generated Questions (SGQ): Developing Mathematical Competence through Online-Assessment. International Journal of Scholarship for Teaching and Learning (IJSTL).Vol 15 (1,8). https://doi.org/10.20429/ijsotl.2021.150108;Caspari-Sadeghi,S., Forster-Heinlein, B., Mägdefrau, J., & Bachl, L. (2021). Sustainable e-assessment in mathematics instruction. In D. Kollosche (Ed.), Proceedings of the Eleventh International Mathematics Education and Society Conference. Vol (1), pp. 57–60. https://doi.org/10.5281/zenodo.5387708 ↵
  6. Universität Passau, „Videos: Passauer MINT-Bonbons“, https://www.mathe-museum.uni-passau.de/videos-passauer-mint-bonbons/ ↵
  7. MINT:Labs Science City Itzling, „(Online) MINTwoch: eine virtuelle Reise in die Salzburger Forschungswelt“, https://www.mintlabs.at/mintwoch/. ↵
  8. A. Beutelspacher, „mathematikum: Mathematik zum Anfassen“ , https://www.mathematikum.de/. ↵
  9. J. Richter-Gebert, „ix-quadrat: Eine Ausstellung des Zentrums Mathematik an der TU München“, https://www.ma.tum.de/de/schulportal/ix-quadrat.html ↵
  10. Technische Sammlungen Dresden, „Erlebnisland Mathematik Dresden“, http://www.erlebnisland-mathematik.de/ ↵
  11. RICHES Project, „RICHES Think Paper 06. Museum education with digital technologies: participation and lifelong learning,“ 2016. [Online]. Available: https://resources.riches-project.eu/riches-think-paper-06-museum-education-with-digital-technologies-participation-and-lifelong-learning/. ↵

About the authors

Contributor photo

name: Prof. Dr. Brigitte Forster-Heinlein

institution: Professur für Angewandte Mathematik, Universität Passau

website: https://www.fim.uni-passau.de/angewandte-mathematik

Brigitte Forster-Heinlein ist Professorin für Angewandte Mathematik an der Universität Passau und forscht in den Bereichen Approximationstheorie, Splines, und Integraltransformationen zur Signal- und Bildverarbeitung. Sie ist Gründerin und Leiterin des Passauer Mathe-Museums, eines Hands-On Museums von Studierenden für Schülerinnen und Schüler. Für ihr Lehrkonzept im Passauer Mathe-Museum wurde sie 2021 vom Stifterverband mit dem Ars Legendi Fakultäten-Preis für Mathematik ausgezeichnet. Das vom BMBF geförderte Projekt SKILL.de weckte ihr Interesse an der Lehr-Lern-Forschung.

Contributor photo

name: Elena Mille

institution: Lehrstuhl für Decentralized Systems Engineering / Forschergruppe: Digital Health, Technische Universität München

Ehem. Wissenschaftliche Mitarbeiterin im Projekt SKILL.de im Passauer Mathe Museum

Lizenz

Icon für Creative Commons Namensnennung-Nicht kommerziell-Weitergabe unter gleichen Bedinungen 4.0 International

Angewandte Mathematik im Passauer Mathe-Museum: Ein Lehrkonzept zur Verzahnung von Mathematik und Didaktik Copyright © by Brigitte Forster-Heinlein und Elena Mille is licensed under a Creative Commons Namensnennung-Nicht kommerziell-Weitergabe unter gleichen Bedinungen 4.0 International, except where otherwise noted.

Dieses Buch teilen